サクサク読めて、
アプリ限定の機能も多数！
アプリで開く
MotivationMachine learning (ML) is a powerful field driven by mathematics. Whether you’rebuilding models, optimizing algorithms, orsimply trying to understand how ML works under the hood, mastering the core equations is essential. Thisblog post is designed to be yourgo-to resource, covering the most critical and “mind-breaking” ML equations—enough to grasp most of the core math behind ML. Eac
機械学習の主要方程式まとめ 8月29日、Chizkiddが「The Most ImportantMachine Learning Equations: A ComprehensiveGuide」と題した記事を公開した。この記事では、機械学習を支える主要な数学的方程式について詳しく紹介されている。 以下に、その内容を簡潔に紹介する。詳しくは原文を参照していただきたい。 1. 確率と情報理論 ベイズの定理 方程式 説明 新しい証拠 $B$ に基づいて仮説 $A$ の確率を更新する手法。分類やベイズ最適化に利用される。Python実装 def bayes_theorem(p_d, p_t_given_d, p_t_given_not_d): p_not_d = 1 - p_d p_t = p_t_given_d * p_d + p_t_given_not_d * p_not_d retur
本書は、データサイエンスに欠かせない微積分・確率・線形代数・統計を、線形回帰・ロジスティック回帰・ニューラルネットワークといった実践的なアルゴリズムと結びつけて学べるハンズオンガイドです。数式による説明を最小限に抑え、SymPy、NumPy、scikit-learnなどのコード例を通じて直感的に理解し、実際に活用する力を養います。後半では、市場で評価されるスキルセットやデータサイエンス分野でのキャリア構築に役立つ実践的アドバイスも提供しています。読み終える頃には、強固な数理基盤と実践力を備え、自信を持って現場で活躍できる力が身についているはずです。 賞賛の声 訳者まえがき まえがき 1章 基礎数学と微積分のおさらい 1.1 数論 1.2 演算の順序 1.3 変数 1.4 関数 1.5 総和 1.6 指数 1.7 対数 1.8 オイラー数と自然対数 1.8.1 オイラー数 1.8.2 自然対
1 中学・高校数学のおさらい～AI・機械学習に必要な計算は四則演算だけ！ 1.1 距離を求めよう～ 四則演算、べき乗、平方根の利用 1.2 複数の点の中心的な位置（重心）を求めよう～ Σ の利用、ベクトル 1.3 予測しよう～関数の利用 1.4 規模の大きな数をうまく扱うには～指数と対数 2 「変化」を見極めよう～微分法の基本から偏微分まで 2.1 この半年で株価はどれだけ上がったか？～平均変化率を求める 2.2 関数の平均変化率を求めよう～平均変化率を文字式で表す 2.3 間隔をどんどん縮めていくと……～いよいよ微分のお話！ 2.4 簡単な例で微分にチャレンジしよう 2.5 二次関数を最小にするx の値を求めよう 2.6 多変数関数を微分する～偏微分にチャレンジ 3 相関・回帰分析超入門～微分法と連立方程式の応用 3.1 部屋の広さと家賃の関係は？～相関係数を求める 3.2 単回帰分析の
この2か月間さる事情があり──いや、本当は大した理由もなく──数学や物理のトピックをいろいろ漁って勉強していた。そして過剰に期待しては幻滅するのをくり返していた。その過程を本記事では紹介する。 アタシっていつもこれだ……。 1.機械学習 2. 数値計算 3. 確率論 4. 数理ファイナンス 5. 非平衡統計力学 6. 量子情報 7. 型理論・ラムダ計算 8. 物性物理 1.機械学習 思ってたのと違った度：10/10 時代の要請と思って石井／上田『わかりやすいパターン認識』（オーム社、第2版2019年）の3部作を読み始めた。そして1巻目を読了した時点で気づく。 「こいつら線形代数とか数理統計学とかを使ってアルゴリズムを組み立てるけど、それがなぜ・どのくらい上手くいくか実験以外で全く説明しねえ！ 仮説もねえ！」 結果、萎え落ちした。有名なビショップ『パターン認識と機械学習 上・下』（丸善出
(ICLR2021) Score-Based Generative Modeling through Stochastic Differential Equations
データサイエンスという分野は、データ収集や可視化などが身近になったことで、より重要になってきています。システムを使ってデータ分析する際、利用者は最終的な結果のみを求めますが、私たちエンジニアはその途中経過についても正しく評価する必要があります。そのためには、中学や高校で学んだ数学の知識が欠かせません。そこで本連載は、高校までに学ぶ基本的な数学知識を使って、データ分析やデータ表現の基礎的な考え方を紹介します。また、既に学んだ数学的基礎からデータの特徴を見つけるためにデータ表現する方法について紹介したいと思います。 はじめに コンピュータでのデータ分析といっても多種多様で、画像や音声、映像、文章などを対象にする場合もあれば、売上値や検査値などの数値を分析する場合もあります。最近では、AIによってさまざまなデータが扱いやすくなり、利用者にとって分かりやすく結果を提示できるようになっています。 そ
はじめに 統計的推論や機械学習において、情報幾何は確率分布の空間をリーマン幾何の枠組みで扱う強力な手法です。本記事では、1次元正規分布を例に、以下の概念をPython（PyTorch）で実装しながら解説します。 フィッシャー情報行列 三次形式（$T_{i,j,k}$） クリストフェル記号（Levi-Civita接続） $α$-接続のクリストフェル記号 リーマン曲率テンソル、スカラー曲率 これらを用いることで、確率分布の幾何構造をより深く理解することができます。 1. フィッシャー情報行列の計算 フィッシャー情報行列は、統計モデルにおける情報量の尺度であり、統計推定の精度を評価する上で重要な役割を果たします。確率分布 $p(x | \theta)$ の対数尤度関数 $\log p(x | \theta)$ に対して、
今回は、いつもと趣向を変えて、勉強・学習方法に特化した記事を記載していく。学歴考察・キャリア考察と違った記事になってしまうのでご容赦頂きたい。 また文章量が膨大になりそうであったので、数回に分けて記載させていただく。 筆者は業務の関係もあって、AI・機械学習に係る学習を2年程度継続して行っている。 一般的にこれらの分野は、理系が多いとされており、文系はあまり見ない。 その中で文系学部卒（経済学部卒）である筆者の学習履歴を記載することは、今後当該分野をリスキリングしたい社会人や学生にとっては有用なのではないかと感じた。 今回は、まずは全体的な概要として、どのような順番で筆者自身がリスキリングを行ってきたのかと言う点を記載させていただく。 まずは、勉強前に筆者が有していた前提知識を記載させていただく。AI・機械学習の分野を習得する上では、主に以下の前提知識が必要であると考える。 ・数学（根本
はじめに こんにちは。データ部ML Product Devチームに所属している谷澤です。 ML Product Devチームは「機械学習を活用した競合優位性のあるプロダクト開発」をミッションとし、プロダクト開発チームと協力して日々開発を行っています。 今回のブログでは、プライベート参加したKaggleコンペティション「Eedi – Mining Misconceptions in Mathematics」で得られた学びについて共有します。 コンペティション概要 タスク Eediコンペティションでは、算数の4択問題が与えられます。問題ごとに1つの正答と3つの誤答が存在し、それぞれの誤答には「どんな誤解（ミスコンセプション）から誤答に至ったか」という情報が紐づけられており、モデルによって「問題とミスコンセプションの対応関係」を予測するのが主な目的です。 たとえば、「12+3×2」という問題で「
多くの学生の声から生まれた，丁寧な解説でわかりやすい今までにない大学教材 理工系の大学2年生の「確率統計」，「数理統計」の半期，もしくは通年の科目で教科書としてお使いいただけます。本書のレイアウトは高校の教科書と同じようになっています。長年高校数学の教科書を発行してきた数研出版ならではの，読んでわかる大学の教科書です。 しかしながら，大学で学ぶ統計学は，大学1年生で学ぶ微分積分学，線形代数学の知識に加え，大学で初めて学ぶ統計学独特の作法や確率の公理を理解することが学習者に「難しい」という印象を与えます。本書では，この「難しい」と感じさせる統計学と数学の関係を懇切丁寧に解説します。統計学の学習に必要な高校数学の復習（Reviewとして数列や関数の極限，集合の記法など）と大学で同時期に学習する微分積分の基礎知識（＋1ポイントとして偏微分，重積分の計算方法など）についての補足があります。 姉妹書
こんにちは👋 長く暑い夏が終わろうとしている今ですが、筆者は秋の季節を満喫しております。 LabBaseでは線形代数学の基礎を使って検索エンジンを構築していますが、レコメンド、検索アルゴリズムによく使われる王道の手法について記事を書くことにしました。 概要 線形代数学の特異値分解（SVD）の知識を活かして、原始的な画像圧縮アルゴリズムをRustで実装します。 SVDとは？ SVDは、線形代数学でよく使われる行列の分解です。行列の分解は、同じマトリックスを他のマトリックスに分けて表現することです。SVDの他に、LU三角分解、QR分解などがあります。 SVDは、あるAというマトリックスの列空間と行空間の固有ベクトルを計算して、それぞれをUとVというマトリックスに収めます。さらに、Σという対角行列に、固有値の平方根を入れます。Vの転置行列をV'と定義しますが、以下の分解になります。 Σの体格行
用語「ダイス係数」について説明。集合間の類似性を評価する尺度で、「2つの集合の共通部分が、それぞれの集合の大きさと比べて、どれだけ大きいか」を測定するために使用される。値が1に近いほど「似ている」を、0に近いほど「似ていない」を意味する。少数の一致でもその正確性が重要視される場面で利用されている。 連載目次 用語解説数学／統計学／機械学習におけるダイス係数（Dice coefficient）とは、2つの集合で「それらの共通部分が、それぞれの集合の大きさと比べて、どれだけ大きいか」の計算値で類似性を表す尺度である。具体的には、「2つの集合の共通部分（＝積集合：∩）」に含まれる要素数を2倍し、それを「2つの集合それぞれの要素数の合計（＝2つの集合に含まれる要素数の平均を2倍した値に相当）」で割ることで計算される（図1）。 このダイス係数の値は、0～1の範囲に正規化され、1は「完全に一致してい
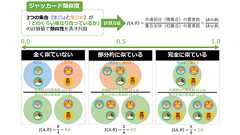
連載目次 用語解説数学／統計学／機械学習におけるジャッカード類似度（JaccardSimilarity）とは、2つの集合が「どのくらい重なり合っているか」の計算値で類似性を表す尺度である。具体的には、「2つの集合の共通部分（＝積集合：∩）」に含まれる要素数を、「2つの集合全体（＝和集合：∪）」に含まれる要素数で割ることで計算される（図1）。このジャッカード類似度の値は、0～1の範囲に正規化され、1なら「完全に同じ集合（＝似ている）」、0なら「全く共通点のない集合（＝似ていない）」を意味する。 ジャッカード類似度は、ジャッカード係数（Jaccard Indexや、Jaccardsimilarity coefficient）とも呼ばれる。これらの用語は同じ概念を指しており、文脈によって使い分けられる。一般的に、JaccardSimilarityは類似度の強調や実際の応用で使われることが
［解決！Python］べき乗を計算するには（**演算子、pow関数、math.pow関数）：解決！PythonPythonでべき乗を計算するには**演算子、組み込みのpow関数、mathモジュールのpow関数を使える。それらの使い方と、振る舞いの違いを紹介する。 # べき乗を計算する3つの方法 base = 2 exp = 10 # **演算子を使う r = base ** exp print(r) # 1024 # 組み込みのpow関数を使う r = pow(base, exp) print(r) # 1024 # mathモジュールのpow関数を使う import math r = math.pow(base, exp) print(r) # 1024.0：math.pow関数では引数は浮動小数点数値に変換される # 組み込みのpow関数ではべき乗した結果をmodで割った剰余を
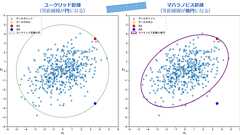
用語「マハラノビス距離」について説明。2点間の距離を計測する方法の一つで、「“普通の距離”（＝ユークリッド距離）を一般化したもの」とも言われる。データの分布（共分散行列）を考慮することで、データのばらつき具合や相関関係を反映した距離を計算できる。異常値や外れ値を識別するために有効であり、特に多次元データにおいて正確な距離測定が可能。 連載目次 用語解説数学／統計学／機械学習におけるマハラノビス距離（Mahalanobis distance）とは、n次元ベクトル（多変量空間）で表現される2点（例えばx＝[x1,x2,...,xn]とy＝[y1,y2,...,yn]）間の「距離」を計算するための方法の一つである（具体的な計算方法は後述する）。マハラノビス距離は、“普通の距離”（厳密にはユークリッド距離、L2ノルム）の計算に「データの分布（厳密には共分散行列）」を加える。これにより、ユークリッ
リリース、障害情報などのサービスのお知らせ
最新の人気エントリーの配信
処理を実行中です
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く
