サクサク読めて、
アプリ限定の機能も多数！
アプリで開く
いやさ、素数って「1とその数自身でしか割り切れない数」じゃん？で、具体例として挙げられるのが3、5、7、11みたいな奇数ばっかりなわけ。 そんな中で堂々と素数面してる「2」、お前だけ偶数じゃん。ずるくない？ だってさ、素数の条件として「2で割り切れちゃダメ」っていうのが暗黙の了解としてあるわけじゃん。素数判定するときも「まず2で割れるかチェックして、割れたら素数じゃない」ってやるわけで。なのに2だけは「俺は2で割り切れるけど素数です」って顔してんの。いや、お前が基準やんけ。 しかも「最小の素数」とか「唯一の偶数の素数」とか、やたら特別扱いされてるし。お前のせいで「素数は全部奇数」っていうシンプルな理解ができないんだよ。数学のテストでも「2は例外として」みたいな注釈入れなきゃいけない。めんどくさい。 3以降の素数たちは、ちゃんと「奇数」っていう仲間意識を持って素数やってんのに、2だけ一人で偶
近年の大規模言語モデル(LLM)は、複雑な問題を段階的に解き明かす「推論モデル」の登場により、数学やコーディングの分野で目覚ましい性能向上を遂げています。しかし、その頑健性、つまり予期せぬ入力への耐性については、まだ十分に解明されていません。スタンフォード大学やCollinearAIなどの研究者チームが、「数学の問題に全く無関係な猫の情報を挿入することでLLMが混乱する」という研究結果を発表しました。 [2503.01781] Cats Confuse Reasoning LLM: Query Agnostic Adversarial Triggers for Reasoning Models https://arxiv.org/abs/2503.01781 ScienceAdviser: Cats confuseAI | Science | AAAS https://www.scie
ふと疑問に思ったことをChatGPTに聞いている。前はGoogleがそれだった。 今「πを小学生の子供に教えるにはどうすればいいですか？」と聞いたら、 「円の直径と円周を実際に測る」と手順を教えてくれた。 そのときに「目的：直径と円周の比が「だいたい3.14」だと気づかせる」とあって、 「π（円周率）って「直径と円周の比」だったんだ・・・！」と知った。 なんか円を扱う時に出てくるパイなやつとしか認識していなかったから意外だった。 今までうっすらあったけど流していた疑問のモヤがスッキリした。 ちなみに子供はいない。 「追記」 多くのコメントありがとうございます・・・。 恥を忍んで自分の持っていたイメージを残しておきます。 もしかしたら私と同じ感覚だった人がいるかもしれないので。 ①小3か4の授業で円を実際に測ることはしていた。 そもそもの質問の「円周率を小学生の子供に教える」が思い浮かんだき
ずんだもんの岐阜案内所 @Zundamon_Gifu @TaT12364250宝くじ100枚如きではまるで狙えないってことがよく分かる実験なのだ・・。 実際にはビー玉何個投入したんだろう？？ 2025-05-11 00:26:27
石野 奈央（なおぽん） @nao_p_on 【問】28人は、35人の何%ですか？ 長男は答えのみ「80%」と書いて、式がないので✕。「ちゃんと式を書きなさい」と注意すると、「待って」と長男。 【長男の解説】 7✕5＝35だよね？7✕4＝28だよね？こんなの見た瞬間80%なのよ。 式、要らないでしょ。 皆さん、彼が何を言ってるかわかりますか？ 2025-03-14 13:15:01
120年以上謎だった難解パズルを解明したと、日米の数学者3人が10日、発表した。「悪魔の証明」とも言われる「ないことの証明」に成功しており、計算機で解くことが困難な図形パズルに新たな解法が得られる可…
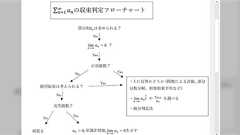
常微分方程式入門 @ode4phys @yakisoba845 @K_animesuki 失礼します。 ものすごく多数の否定的意見がついていると思いますが、私は「自分で試してみる」と書かれた点に好感を持ちました。 この手の「フローチャート」は、他人からの借り物や押し付けになると失敗しがちです。しかし自分で自分の理解に合ったものを作るなら役立つことが期待できるので。 2025-02-16 12:40:35
九九は掛け算の入門ではない 【西成先生】3を4回足すのは頭の中で計算できますね。でも、「9を8回足せ」とか、「2980を543回足せ」になると大変です。そこで昔の人がいいアイデアを思いついたんです。「毎回足すのは面倒くさい。だったら1から9までの数同士の組み合わせを丸暗記すればいい。81パターンならなんとかなるだろう」って。いわゆる九九のことです。 【郷さん】画期的な方法を思いついたとかではなく？ 【西成先生】暗記という力業にすぎないんです（笑）。でも、こうやって81パターンの掛け算を暗記したり、あらかじめメモをしておく方法が広まったことで、そろばんや筆算を使ってどんなに大きな数でも掛け算ができるようになったんです。これは革命的な出来事です。 だから九九って「掛け算の入門」みたいな位置づけでは決してなくて、掛け算の本家本丸です。昔の人からすれば「え？ なんでこの計算を暗算できるの？ 超天才
じゃむまる │10代で1番Dify詳しい人 @jammaru_labAIの進化で、勉強効率が本当に劇的に上がった。学校の勉強も同じで、昔は数学の問題が分からなかったら答えを見て、詳しい解説を友達に聞く必要があったけど、今はGPTやo1に問題の画像をアップするだけで、めっちゃ丁寧に解説してくれる。効率が爆上がりしてるから、今の中学生とかが羨ましい。 2025-01-16 11:19:36 じゃむまる │10代で1番Dify詳しい人 @jammaru_labAI使ったら頭が悪くなると思ってる人居るかもだけど、AIは使い方次第で勉強にもめっちゃ使える。上手く使えればかなり勉強の効率も上がる。何事も使い方次第。 2025-01-16 11:20:50 じゃむまる │10代で1番Dify詳しい人 @jammaru_labAIは本当に使い方次第。ある人は勉強法にAIを取り入れることで、これまでに
このコーナーでは、2014年から先端テクノロジーの研究を論文単位で記事にしているWebメディア「Seamless」（シームレス）を主宰する山下裕毅氏が執筆。新規性の高い科学論文を山下氏がピックアップし、解説する。 X： ＠shiropen22023年、米国の高校生ネキヤ・ジャクソンさんとカルセア・ジョンソンさんは、地元の高校のコンテストで驚くべき成果を披露した。それは、三角関数を用いてピタゴラスの定理を証明するという方法の発見であった。 「a^2+b^2=c^2」で表されるピタゴラスの定理は、よく知られている数学の基本定理である。この式は、直角三角形において、最も長い辺（斜辺）の2乗が、残りの二辺の2乗の和に等しいことを示している。 これまで数多くの数学者たちが代数学や幾何学を用いてこの定理を証明してきたが、三角関数による証明はより難しかった。三角関数の基本公式自体がピタゴラスの定理を前
長野県大町市に住む折り紙作家 布施知子さん。 これまでに制作した作品は国内だけでなく、世界中から評価され注目を集めています。 今、制作した折り紙の技術が教育や産業などさまざまな分野の可能性を広げています。 彼女の折り紙の世界を取材しました。 「無限折り」「螺旋」「コイル折り」 世界的に評価を受ける作品たち 流れゆく川を表現した、この作品。 実はこれ、20メートルの1枚の紙から出来ています。 無数の折り目を、複雑に重ねる「無限折り」という技法で作られました。 制作したのは大町市に住む折り紙作家の布施知子さん。 37年前に、自然に囲まれた山あいの古民家に移住し、個性あふれる作品を世に送り出してきました。 何重にも細かく規則的に折り続けることで生み出す「螺旋」。 筒状にした紙を、つぶしながら折り込んだ「コイル折り」 その作品はヨーロッパ各地で個展が開かれるなど、海外からも高い評価を受けています。
このコーナーでは、2014年から先端テクノロジーの研究を論文単位で記事にしているWebメディア「Seamless」（シームレス）を主宰する山下裕毅氏が執筆。新規性の高い科学論文を山下氏がピックアップし、解説する。 X： ＠shiropen2 英インペリアル・カレッジ・ロンドン（ICL）の教授であり、数学者のケビン・バザードさんの単著論文「Grothendieck’s use of equality」は、数学者が等式の概念をどのように使用しているか、そしてそれが数学の形式化を試みる際にどのような影響を与えるかについて議論した研究報告である。 バザードさんは「現状、数学者は等式の概念を曖昧に使っており、近年のコンピュータプログラムによる証明（形式化）においてその曖昧さが障害になっている」と指摘する。 「＝」（等号）にみる一般的な等式の定義は、両辺が同じ数学的対象を表しており、一方から他方への論
115人の参加者を対象に、1～9までの数字を使って300桁のランダムな数列を2回生成してもらう実験を行った。参加者には、数字の出現頻度ができるだけ均等になるよう意識しながら、なるべく予測不能な数列を生成するよう求めた。 そして、2つの数列の類似度を定量化する独自の手法を用いて分析したところ、わずか300桁の数列だけでも、同一人物が生成した数列と、別人が生成した数列を、96.5％の高い精度で見分けられることが分かった。 この現象は、個人によって好む数字の並びや、避ける数字の並びが異なることに起因しており、1週間後に再度実験を行っても、その傾向は変わらなかった。つまり、数列に現れる規則性は、その人固有の認知的な「指紋」のようなものだといえる。 また、この個人差が、単なる認知能力の違いでは説明できないこと、また、個人になじみ深い数字の並び（電話番号や郵便番号、生年月日など）が影響しているわけでも
このコーナーでは、2014年から先端テクノロジーの研究を論文単位で記事にしているWebメディア「Seamless」（シームレス）を主宰する山下裕毅氏が執筆。新規性の高い科学論文を山下氏がピックアップし、解説する。Twitter: ＠shiropen2 ペンシルベニア大学などに所属する研究者らが発表した論文「Information content ofnotetransitions in themusic of J. S. Bach」は、音楽作品を情報ネットワークへと変換し、作品が内包する情報量と伝達効率を調査した研究報告である。この研究では、バッハの楽曲を情報ネットワークとしてモデル化し、楽曲が持つ情報量とその情報をいかに効率よく伝達するかを定量的に評価する。 手法の第一歩として、楽曲の各音符をネットワーク上のノードとして捉え、音符間の遷移をエッジで結び付けている。このエッジは指向
「ピータースのコイントス」は「大勢の参加者の平均」を求めると必ずプラスになる賭け事に見えるのに、実際に何度も挑むと大敗を喫することになる魔のコインゲームです。ピータースのコイントスを考案したオーレ・ピータース氏は、当該ゲームの恐ろしさが一発で分かるシミュレーターを公開しています。 The infamous coin toss – Ergodicity economics https://ergodicityeconomics.com/2023/07/28/the-infamous-coin-toss/ ピータースのコイントスのルールは以下の通り。 ・所持金は100ドルからスタート ・コインを投げて表が出たら所持金の50％を追加でもらえる ・コインを投げて裏が出たら所持金の40％を没収される ・コイントスは何回繰り返してもOK ルールをパッと読むと「もらえる割合の方が没収される割合よりも大き
4月に行われた小6と中3が対象の全国学力・学習状況調査の結果を、文部科学省が公表した。小6の算数では、図形の構成要素に着目して考える問題などに課題がみられたという。中3の数学も合わせ、子どもの学力の…
何十年も探し求められた「アインシュタイン」のタイルがついに発見されたそうだ。 それは13の辺を持つジグソーパズルのような図形で、どれだけ並べても、絶対に同じパターンが繰り返されることはない。数学の世界で「非周期的モノタイル」と呼ばれるこの形状の発見は、数学の歴史の革新的発見（ブレイクスルー）と称されている。 この図形の不思議さとすごさ、面白さを説明していこう。 非周期的タイルとは何か？ 「アインシュタイン」とは言っても、あの天才物理学者アルベルト・アインシュタインのことではない。ドイツ語で「1つの石」のことで、つまりは1枚のタイルであることを意味するものだ。 これについて、発見者の1人であるカナダ、ウォータールー大学のクレイグ・カプラン教授は、「私たちは史上初の本物の”非周期的モノタイル”を紹介しています」と声明で述べている。 「非周期的タイル」とは何か？ それは平面を隙間なく、かつ重な
リリース、障害情報などのサービスのお知らせ
最新の人気エントリーの配信
処理を実行中です
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く
