この広告は、90日以上更新していないブログに表示しています。
つばきファクトリーで本当ににらめっこが強いのは誰か
行くぜ!つばきファクトリー#76でにらめっこ対決をしていました。個人の対戦成績を列挙すると、
村田x o土居石井o x豫風小野x o秋山石井x o小野田村田o x八木小野x o小野田谷本o x福田豫風o x河西秋山o x村田土居x o小野谷本o x石井八木x o石井小野田o x小野福田o x村田福田o x土居小野田x o豫風河西o x秋山
です。これを個人の戦績に直すと、
| 1位 | 谷本 | 2勝0敗 |
| 2位 | 小野田 | 3勝1敗 |
| 3位 | 豫風 | 2勝1敗 |
| 3位 | 秋山 | 2勝1敗 |
| 3位 | 福田 | 2勝1敗 |
| 6位 | 石井 | 2勝2敗 |
| 6位 | 河西 | 1勝1敗 |
| 8位 | 土居 | 1勝2敗 |
| 9位 | 村田 | 1勝3敗 |
| 9位 | 小野 | 1勝3敗 |
| 11位 | 八木 | 0勝2敗 |
勝率で順位付けしています。
しかし、強い人と当たるとどうしても成績が悪くなりますよね。こういうときよくElo Ratingという指標が用いられますが、あまりに誤差が大きそうなのでMCMCを使ってレーティングを計算してみました。
| 1位 | 谷本 | 1764.4±111.3 |
| 2位 | 豫風 | 1619.3±76.6 |
| 3位 | 小野田 | 1619.3±76.5 |
| 4位 | 石井 | 1619.2±76.6 |
| 5位 | 河西 | 1556.0±77.0 |
| 6位 | 福田 | 1546.6±119.4 |
| 7位 | 秋山 | 1494.5±77.4 |
| 8位 | 小野 | 1433.9±80.3 |
| 9位 | 土居 | 1368.3±82.9 |
| 10位 | 村田 | 1297.5±90.3 |
| 11位 | 八木 | 1189.2±116.5 |
mean±σです。勝率とは違う順位になることが分かるでしょう。2~4位は同じ分布です。それから、分布は広くてこんな少ない対戦では本当の強さは分からないことが分かります。

# coding: utf-8from __future__import annotationsfrom itertoolsimport groupbyfrom collectionsimport defaultdictfrom fractionsimport Fractionimport sysimport pandasas pdimport numpyas npdefcalculate_frequencies(trace, players, num_bins=20): frequencies = {}for playerin players: samples = trace[player] freq, edges = np.histogram(samples, bins=num_bins) bin_centers = (edges[:-1] + edges[1:]) /2 frequencies[f"{player}_freq"] = freq frequencies[f"{player}_bins"] = bin_centersreturn frequenciesdefexport_frequencies_to_excel(frequencies, filename='player_skill_frequencies.xlsx'):# 各プレイヤーのビンセンターを同じにするため、最小および最大範囲を計算 min_bin =min(min(freq)for freqin frequencies.values()if'_bins'in freq) max_bin =max(max(freq)for freqin frequencies.values()if'_bins'in freq) bin_centers = np.linspace(min_bin, max_bin,len(frequencies[next(iter(frequencies))])) data = {}for playerin players: freq = frequencies[f"{player}_freq"] bins = frequencies[f"{player}_bins"] data[f"{player}_freq"] = np.interp(bin_centers, bins, freq) data[f"{player}_bins"] = bin_centers df = pd.DataFrame(data) df.to_excel(filename, index=False)print(f'Data exported to {filename}')defexport_frequencies_to_excel(frequencies, filename='player_skill_frequencies.xlsx'): df = pd.DataFrame(frequencies) df.to_excel(filename, index=False)print(f'Data exported to {filename}')defexport_trace_to_excel(trace, players, filename='player_skills.xlsx'): data = {player: trace[player]for playerin players} df = pd.DataFrame(data) df.to_excel(filename, index=False)print(f'Data exported to {filename}')colors = {'谷本':'#e6e6fa','小野':'#50c878','小野田':'#ffdab9','秋山':'#ff6347','河西':'#800080','八木':'#ffa500','福田':'#4169e1','豫風':'#ffdb58','石井':'#ffffff','村田':'#ffb6c1','土居':'#00ff7f' }# -> (win, lose)defparse_result(line:str) ->tuple[str,str]:for i, cinenumerate(line):if cnotin'ox':continue player1 = line[:i] player2 = line[i+3:]if c =='o':return (player1, player2)else:return (player2, player1)return ('','')defread_results(path:str) ->list[tuple[str,str]]:withopen(path,'r')as f:return [ parse_result(line.rstrip())for linein f ]defadd(v:tuple[int,int], w:tuple[int,int]) ->tuple[int,int]:return (v[0] + w[0], v[1] + w[1])defdetermin_ranking(resutls:list[tuple[str,str]] ) ->list[tuple[int,str,int,int]]: dic:dict[str,tuple[int,int]] = defaultdict(lambda : (0,0))for player1, player2in results: dic[player1] = add(dic[player1], (1,0)) dic[player2] = add(dic[player2], (0,1)) players = [ (p, w, l)for p, (w, l)in dic.items() ] players.sort(key=lambda v: Fraction(v[1], v[1]+v[2]), reverse=True) ranks:list[tuple[int,str,int,int]] = [] rank =1for r, vin groupby(players, key=lambda v: Fraction(v[1], v[1]+v[2])): ps =list(v)for p, w, lin ps: ranks.append((rank, p, w, l)) rank +=len(ps)return ranksdefprint_ranks(ranks:list[tuple[int,str,int,int]]):for rank, player, win, losein ranks: args = (rank, player, win, lose)print('|%d位|%s|%d勝%d敗|' % args)import pymc3as pmimport numpyas np# モデルの構築import pymc3as pmdefbuild_model(matches, players, initial_rating, sigma): model = pm.Model()with model:# 各プレイヤーの実力を正規分布でモデル化 skills = { player: pm.Normal(player, mu=initial_rating, sigma=sigma)for playerin players }# 対戦結果の尤度関数を定義for i, (player1, player2)inenumerate(matches): skill_diff = skills[player1] - skills[player2] prob_win = pm.math.sigmoid(skill_diff) pm.Bernoulli(f'{i}', p=prob_win, observed=1)return modeldefsample_model(model, num_samples, num_tune): trace = pm.sample(num_samples, tune=num_tune, cores=2, model=model)return tracedefprint_rate(trace, players): rates = [ (np.mean(trace.get_values(player)), player)for playerin players ] rates.sort(reverse=True)for i, (rate, player)inenumerate(rates,1):print("%d位 %6s %.2f" % (i, player, rate))import matplotlib.pyplotas pltimport arvizas azfrom matplotlibimport font_managerdefplot_results(trace, players, path_img):# 日本語フォントを指定 font_path ='/usr/share/fonts/truetype/takao-gothic/TakaoPGothic.ttf' font_prop = font_manager.FontProperties(fname=font_path) plt.rcParams['font.family'] = font_prop.get_name() plt.figure(figsize=(10,6))for playerin players: az.plot_posterior(trace, var_names=[player], ref_val=1500, hdi_prob=0.94, ax=plt.gca()) plt.title('Skill Distributions of Players') plt.xlabel('Skill Level') plt.ylabel('Density') plt.legend(players) plt.savefig(path_img) plt.close()print(f'Saved plot to {path_img}')path = sys.argv[1]results = read_results(path)players =list(set(pfor vin resultsfor pin v))ranks = determin_ranking(results)print_ranks(ranks)model = build_model(results, players,1500,200)trace = sample_model(model,2000,1000)print_rate(trace, players)plot_results(trace, players,"N-1.png")# 頻度の計算frequencies = calculate_frequencies(trace, players)# データのエクスポートexport_frequencies_to_excel(frequencies)
年の差ラジオのWOC
https://radio.rcc.jp/toshinosa/
ザ・ギース尾関高文とOCHA NORMA広本瑠璃の年の差ラジオをでゲームをやっていましたが、全く勝てそうになかったのに勝ちました。勝つ確率はどれくらいなのか算出します。
ルールとしては明確ではなかったですが、プレーヤー1は1イニングに1~20のどれかの点数が同確率で入る、プレーヤー2はアウトが1/2、単打が1/3、ホームランが1/6で起こるとします。イニングが終わって10点以上差がついていたらコールドです。
まず、ランダムに1億回プレイしてみましょう。
from __future__import annotationsfrom itertoolsimport *from collectionsimport Counterimport randomimport sysfrom enumimport Enumfrom typingimport List, TupleState = Tuple[int,int,int]classAction(Enum): OUT =1 HIT =2 HOMERUN =3@staticmethoddefselect_randomly(): r = random.randrange(1,7)if r <=3:return Action.OUTelif r <=5:return Action.HITelse:return Action.HOMERUNdeftransit(s: State, a: Action) -> State: (score, out, base) = sif a == Action.OUT:return (score, out +1, base)elif a == Action.HIT:if base ==3:return (score +1, out, base)else:return (score, out, base +1)else:return (score + base +1, out,0)defplay1_randamly() ->int:return random.randrange(1,21)defplay2_randomly() ->int: s = (0,0,0)whileTrue: s = transit(s, Action.select_randomly())if s[1] ==3:return s[0]defplay_randomly() ->str: score1 =0 score2 =0for _inrange(9): score1 += play1_randamly() score2 += play2_randomly()if score1 >= score2 +10:return'Lose'elif score2 >= score1 +10:return'Win'if score1 > score2:return'Lose'elif score1 < score2:return'Win'else:return'Draw'N =int(sys.argv[1])c = Counter(play_randomly()for _inrange(N))print(c)
Counter({'Lose': 99860253, 'Win': 139604, 'Draw': 143})勝つ確率は0.14%程度のようです。
次に、真面目に確率計算をします。最初にプレーヤー2が1イニングに何点入るかの確率を求めます。ただし、181点以上入ったら必ず勝つので、181点以上はまとめて181点とします。
from __future__import annotationsfrom functoolsimportreducefrom itertoolsimport *from collectionsimport Counterimport randomimport sysfrom enumimport Enumfrom typingimport List, TupleState = Tuple[int,int,int]classAction(Enum): OUT =1 HIT =2 HOMERUN =3@staticmethoddefprobability(a: Action):if a == Action.OUT:return3 /6elif a == Action.HIT:return2 /6else:return1 /6deftransit(s: State, a: Action) -> State: (score, out, base) = sif a == Action.OUT:return (score, out +1, base)elif a == Action.HIT:if base ==3:return (score +1, out, base)else:return (score, out, base +1)else:return (score + base +1, out,0)defprobs_inning(N:int) ->list[float]: probs:list[float] = [0.0] * (N +2) c: Dict[State,float] = Counter() c[(0,0,0)] =1.0while c: new_c: Dict[State,float] = Counter()for s0, p0in c.items():for actionin Action: s1 = transit(s0, action) score, out, base = s1 p1 = p0 * Action.probability(action)if out ==3: probs[score] += p1elif score > N:passelse: new_c[s1] += p1 c = new_cprint(1.0 -sum(probs[:11]))# 11点以上取る確率 probs[N+1] = probs[N]# 半分ずつ減っていくのでたぶんこれくらいreturn probsdefdecide_probs(): probs1 = [0.0] + [1/20] *20 probs2 = probs_inning(180)# 181点上なら必ず勝つ probs = [0.0] *3# [Lose, Win, Draw] scores = { (0,0):1.0 }for iinrange(9): new_scores: Dict[tuple[int,int],float] = Counter()for (score1, score2), p0in scores.items():for s1, s2in product(range(1,21),range(182)): prob1 = probs1[s1] prob2 = probs2[s2] new_score1 = score1 + s1 new_score2 = score2 + s2 p = p0 * prob1 * prob2if new_score1 >= new_score2 +10: probs[0] += p# Loseelif new_score2 >= new_score1 +10: probs[1] += p# Winelse: new_scores[(new_score1, new_score2)] += p scores = new_scoresfor (score1, score2), pin scores.items():if score1 > score2: probs[0] += p# Loseelif score1 < score2: probs[1] += p# Winelse: probs[2] += p# Drawprint("Lose: %.6f, Win: %.6f, Draw: %.2e" %tuple(probs))decide_probs()
まず、プレーヤー2が1イニングに11点以上取る確率は、0.6%程度です。
そして、
Lose: 0.998606, Win: 0.001392, Draw: 1.39e-06
ランダムにプレイしたときとほとんど変わらないですね。
ハロプロ楽曲大賞2019集計(3)
投票者がどのユニットの曲に入れたかを、自分の推しのユニットごとに集計した。
兼任は当分配で。
グラフは、累積の割合。
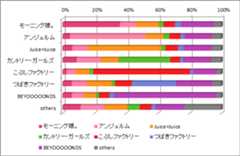
どのユニットも、自ユニットに最も入れているのは変わらないが、その次に入れているユニットかを見てみると、BEYOOOOONDSヲタ以外はBEYOOOOONDSであることがわかる。
順位を表にすると分かりやすい。

以下に、全てのデータを示す。
,モーニング娘。,アンジュルム,Juice=Juice,カントリー・ガールズ,こぶしファクトリー,つばきファクトリー,BEYOOOOONDS,othersモーニング娘。,6635.5,1807.75,2677.25,546.5,1317.0,706.25,3858.5,811.25アンジュルム,220.75,2258.0,543.5,173.5,332.0,122.0,820.25,280.0Juice=Juice,262.5,409.0,1990.0,118.0,335.5,153.5,757.5,264.0カントリー・ガールズ,138.25,231.5,177.25,508.0,96.75,29.75,278.0,95.5こぶしファクトリー,55.5,110.5,182.5,53.0,1262.0,39.5,307.5,59.5つばきファクトリー,92.5,149.5,254.0,32.0,171.0,443.5,365.5,92.0BEYOOOOONDS,260.5,319.5,345.75,92.75,298.75,119.25,2861.75,146.75others,1068.0,1382.5,1384.75,715.5,695.75,247.5,1696.0,2185.0
ハロプロ楽曲大賞2019集計(2)
ハロプロ楽曲大賞の投票者数の減少は本当にカントリー・ガールズヲタのせいなのか?
ハロプロ楽曲大賞の投票人数が去年は一昨年に比べて約400人減ったという。推しメン部門では、3905人から3511人になった。
これについて、カントリー・ガールズのヲタが投票しなくなったから、という言説をどこかで見た。これを検証してみる。
まず、一昨年の得票数は、
| 森戸知沙希 | 85票 |
| 船木結 | 62票 |
| 梁川奈々美 | 57票 |
| 山木梨沙 | 54票 |
| 小関舞 | 31票 |
| 嗣永桃子 | 29票 |
と、全体で318票で、400票に満たない。
では、カントリー・ガールズヲタは、他のユニットのヲタより減少しているのだろうか。
一昨年と去年で同じIDの投票者を追いかければ分かるかと思ったが、実は同じ投票者でもIDは変わるらしい。そこで、ニックネームで追いかけることにした。
では、ニックネームはどれくらい重複するだろうか。
一昨年は、ニックネームは3610あり、ユニークな(一度しか現れない)ニックネームは3405。去年は、ニックネームは3287あり、ユニークなニックネームは3129。
そして、一昨年のユニークなニックネームの投票者3405人が去年どうしたかを調べた。
全体では、1729人が投票、1676人が不明(ニックネームを変えているかもしれないので)。
では、カントリー・ガールズヲタの投票者はどうしたのか調べた。
| 名前 | 投票 | 不明 |
| 梁川奈々美 | 30 | 21 |
| 小関舞 | 8 | 18 |
| 嗣永桃子 | 13 | 12 |
| 森戸知沙希 | 36 | 34 |
| 山木梨沙 | 31 | 22 |
| 船木結 | 23 | 31 |
| 合計 | 141 | 138 |
全体の投票・不明の割合と変わらない。カントリー・ガールズヲタが投票しなかったという証拠は見つからなかった。
ついでに、各ヲタが推し変したかを調べた。
梁川奈々美 ->梁川奈々美 9 小林萌花 3山木梨沙 3 西田汐里 2 その他 13
小関舞 -> 小関舞 6 その他 2
嗣永桃子 ->嗣永桃子 8 その他 5
船木結 ->船木結 16 江口紗耶 2 その他 5
森戸知沙希 ->森戸知沙希 29野村みな美 2 その他 5
山木梨沙 ->山木梨沙 26 その他 5
ちなみに、一昨年上位は、
佐藤優樹 ->佐藤優樹 134 その他 26
小田さくら ->小田さくら 57 その他 9
宮本佳林 ->宮本佳林 65 その他 14
加賀楓 ->加賀楓 74 その他 13
和田彩花 ->和田彩花 19中西香菜 4上國料萌衣 4 その他 27
ニックネームで追うのもそんなに悪くないことが分かる。
ハロプロ楽曲大賞2019集計(1)
上位の曲に、どのユニットのヲタが投票したかをポイントで集計してみた。
兼任の3人は、等分。
| song | モーニング娘。'19 | アンジュルム | Juice=Juice | カントリー・ガールズ | こぶしファクトリー | つばきファクトリー | BEYOOOOONDS | others |
| 「ひとりで生きられそう」って それってねえ、褒めているの? | 1266.0 | 343.5 | 1066.5 | 84.0 | 126.0 | 136.0 | 158.0 | 401.5 |
| 「ひとりで生きられそう」って それってねえ、褒めているの? (New Vocal Ver.) | 66.75 | 26.75 | 39.5 | 5.0 | 11.5 | 18.0 | 17.0 | 15.0 |
| ニッポンノD・N・A! | 805.75 | 260.0 | 231.0 | 87.25 | 82.0 | 108.5 | 391.0 | 268.0 |
| 眼鏡の男の子 | 673.0 | 211.5 | 158.0 | 45.5 | 60.0 | 58.0 | 481.0 | 187.0 |
| 青春Night | 1296.5 | 89.5 | 89.0 | 60.0 | 16.0 | 35.0 | 73.0 | 147.0 |
| 赤いイヤホン | 378.75 | 641.25 | 133.0 | 64.0 | 45.0 | 46.0 | 62.5 | 208.0 |
| 都営大江戸線の六本木駅で抱きしめて | 480.0 | 147.25 | 120.0 | 75.75 | 75.5 | 94.0 | 312.0 | 200.0 |
| 人生Blues | 1033.0 | 56.5 | 85.0 | 34.0 | 18.0 | 24.5 | 51.5 | 127.5 |
| I surrender 愛されど愛 | 873.0 | 37.75 | 32.0 | 12.25 | 10.0 | 14.0 | 34.5 | 87.5 |
| 恋してみたくて | 840.25 | 28.0 | 34.5 | 28.75 | 8.0 | 12.0 | 20.5 | 97.0 |
| 微炭酸 | 240.5 | 80.5 | 342.5 | 35.0 | 17.0 | 59.5 | 29.0 | 117.0 |
| 消せやしないキモチ | 178.75 | 66.25 | 83.0 | 31.0 | 279.5 | 31.5 | 54.5 | 124.5 |
| 人生、すなわちパンタ・レイ | 153.25 | 419.0 | 49.5 | 39.75 | 10.0 | 21.5 | 33.5 | 107.0 |
| 全然起き上がれないSUNDAY | 225.5 | 291.5 | 64.5 | 40.5 | 11.5 | 19.0 | 55.5 | 78.5 |
| ふわり、恋時計 | 259.0 | 68.75 | 71.5 | 14.75 | 15.0 | 203.5 | 52.0 | 79.0 |
| One Summer Night ~真夏の決心~ | 161.75 | 82.75 | 58.5 | 190.0 | 22.5 | 16.0 | 31.5 | 82.0 |
| ハルウララ | 179.25 | 69.0 | 56.0 | 16.25 | 164.0 | 47.5 | 41.5 | 64.0 |
| 三回目のデート神話 | 195.0 | 51.75 | 73.0 | 13.75 | 19.5 | 194.0 | 31.5 | 39.0 |
| 元年バンジージャンプ | 117.25 | 27.75 | 68.0 | 21.5 | 16.5 | 14.5 | 212.0 | 66.0 |
| 弱気女子退部届 | 126.25 | 54.5 | 34.5 | 152.25 | 16.5 | 15.0 | 27.5 | 103.5 |



