Swiss Table#
A specialized hash table implementation used to dynamically map combinations ofkey field values to a dense set of integer ids. Ids can later be used in placeof keys to identify groups of rows with equal keys.
Introduction#
Hash group-by in Arrow uses a variant of a hash table based on a data structurecalled Swiss table. Swiss table uses linear probing. There is an array of slotsand the information related to inserted keys is stored in these slots. A hashfunction determines the slot where the search for a matching key will startduring hash table lookup. Then the slots are visited sequentially, wrappingaround the end of an array, until either a match or an empty slot is found, thelatter case meaning that there is no match. Swiss table organizes the slots inblocks of 8 and has a design that enables data level parallelism at the blocklevel. More precisely, it allows for visiting all slots within a block at onceduring lookups, by simply using 64-bit arithmetic. SIMD instructions can furtherenhance this data level parallelism allowing to process multiple blocks relatedto multiple input keys together using SIMD vectors of 64-bit elements. Occupiedslots within a block are always clustered together. The name Swiss table comesfrom likening resulting sequences of empty slots to holes in a one dimensionalcheese.
Interface#
Hash table used in query processing for implementing join and group-by operatorsdoes not need to provide all of the operations that a general purpose hash tablewould. Simplified requirements can help achieve a simpler and more efficientdesign. For instance we do not need to be able to remove previously insertedkeys. It’s an append-only data structure: new keys can be added but old keys arenever erased. Also, only a single copy of each key can be inserted - it is likestd::map in that sense and notstd::multimap.
Our Swiss table is fully vectorized. That means that all methods work on vectorsof input keys processing them in batches. Specialized SIMD implementations ofprocessing functions are almost always provided for performance criticaloperations. All callback interfaces used from the core hash table code are alsodesigned to work on batches of inputs instead of individual keys. The batch sizecan be almost arbitrary and is selected by the client of the hash table. Batchsize should be the smallest number of input items, big enough so that thebenefits of vectorization and SIMD can be fully experienced. Keeping it smallmeans less memory used for temporary arrays storing intermediate results ofcomputation (vector equivalent of some temporary variables kept on the stack).That in turn means smaller space in CPU caches, which also means less impact onother memory access intensive operations. We pick 1024 as the default size ofthe batch. We will call it amini-batch to distinguish it from potentiallyother forms of batches used at higher levels in the code, e.g. when schedulingwork for worker threads or relational operators inside an analytic query.
The main functionality provided by Swiss table is mapping of arbitrarily complexkeys to unique integer ids. Let us call itlookup-or-insert. Given asequence of key values, return a corresponding sequence of integer ids, suchthat all keys that are equal receive the same id and for K distinct keys theinteger ids will be assigned from the set of numbers 0 to (K-1). If we find amatching key in a hash table for a given input, we return thekey idassigned when the key was first inserted into a hash table. If we fail to findan already inserted match, we assign the first unused integer as a key id andadd a new entry to a hash table. Due to vectorized processing, which may resultin out-of-order processing of individual inputs, it is not guaranteed that ifthere are two new key values in the same input batch and one of them appearsearlier in the input sequence, then it will receive a smaller key id. Additionalmapping functionality can be built on top of basic mapping to integer key id,for instance if we want to assign and perhaps keep updating some values to allunique keys, we can keep these values in a resizable vector indexed by obtainedkey id.
The implementation of Swiss table does not need to have any information relatedto the domain of the keys. It does not use their logical data type orinformation about their physical representation and does not even use pointersto keys. All access to keys is delegated to a separate class or classes thatprovide callback functions for three operations:
computing hashes of keys;
checking equality for given pairs of keys;
appending a given sequence of keys to a stack maintained outside of Swisstable object, so that they can be referenced later on by key ids (key ids willbe equal to their positions in the stack).
When passing arguments to callback functions the keys are referenced usinginteger ids. For the left side - that is the keys present in the inputmini-batch - ordinal positions within that mini-batch are used. For the rightside - that is the keys inserted into the hash table - these are identified bykey ids assigned to them and stored inside Swiss table when they were firstencountered and processed.
Diagram with logical view of information passing in callbacks:

Hash table values for inserted keys are also stored inside Swiss table. Becauseof that, hash table logic does not need to ever re-evaluate the hash, and thereis actually no need for a hash function callback. It is enough that the callerprovides hash values for all entries in the batch when calling lookup-or-insert.
Basic architecture and organization of data#
The hash table is an array ofslots. Slots are grouped in groups of 8 calledblocks. The number of blocks is a power of 2. The empty hash table startswith a single block, with all slots empty. Then, as the keys are gettinginserted and the amount of empty slots is shrinking, at some point resizing ofthe hash table is triggered. The data stored in slots is moved to a new hashtable that has the double of the number of blocks.
The diagram below shows the basic organization of data in our implementation ofSwiss table:
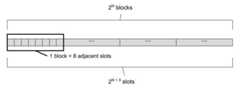
N is the log of the number of blocks,\(2^{N+3}\) is the number of slots andalso the maximum number of inserted keys and hence (N + 3) is the number of bitsrequired to store a key id. We will refer to N as thesize of the hash table.
Index of a block within an array will be calledblock id, and similarly indexof a slot will beslot id. Sometimes we will focus on a single block andrefer to slots that belong to it by using alocal slot id, which is an indexfrom 0 to 7.
Every slot can either beempty or store data related to a single insertedkey. There are three pieces of information stored inside a slot:
status byte,
key id,
key hash.
Status byte, as the name suggests, stores 8 bits. The highest bit indicates ifthe slot is empty (the highest bit is set) or corresponds to one of insertedkeys (the highest bit is zero). The remaining 7 bits contain 7 bits of key hashthat we call astamp. The stamp is used to eliminate some false positiveswhen searching for a matching key for a given input. Slot also storeskey id,which is a non-negative integer smaller than the number of inserted keys, that isused as a reference to the actual inserted key. The last piece of informationrelated to an inserted key is itshash value. We store hashes for all keys,so that they never need to be re-computed. That greatly simplifies someoperations, like resizing of a hash table, that may not even need to look at thekeys at all. For an empty slot, the status byte is 0x80, key id is zero and thehash is not used and can be set to any number.
A single block contains 8 slots and can be viewed as a micro-stack of up to 8inserted keys. When the first key is inserted into an empty block, it will occupya slot with local id 0. The second inserted key will go into slot number 1 and soon. We use N highest bits of hash to get an index of astart block, whensearching for a match or an empty slot to insert a previously not seen key whenthat is the case. If the start block contains any empty slots, then the searchfor either a match or place to insert a key will end at that block. We will callsuch a block anopen block. A block that is not open is a full block. In thecase of full block, the input key related search may continue in the next blockmodulo the number of blocks. If the key is not inserted into its start block, wewill refer to it as anoverflow entry, other entries beingnon-overflow.Overflow entries are slower to process, since they require visiting more than oneblock, so we want to keep their percentage low. This is done by choosing therightload factor (percentage of occupied slots in the hash table) at whichthe hash table gets resized and the number of blocks gets doubled. By tuning thisvalue we can control the probability of encountering an overflow entry.
The most interesting part of each block is the set of status bytes of its slots,which is simply a single 64-bit word. The implementation of efficient searchesacross these bytes during lookups require using either leading zero count ortrailing zero count intrinsic. Since there are cases when only the first one isavailable, in order to take advantage of it, we order the bytes in the 64-bitstatus word so that the first slot within a block uses the highest byte and thelast one uses the lowest byte (slots are in reversed bytes order). The diagrambelow shows how the information about slots is stored within a 64-bit statusword:

Each status byte has a 7-bit fragment of hash value - astamp - and an emptyslot bit. Empty slots have status byte equal to 0x80 - the highest bit is set to1 to indicate an empty slot and the lowest bits, which are used by a stamp, areset to zero.
The diagram below shows which bits of hash value are used by hash table:

If a hash table has\(2^{N}\) blocks, then we use N highest bits of a hashto select a start block when searching for a match. The next 7 bits are used asa stamp. Using the highest bits to pick a start block means that a range of hashvalues can be easily mapped to a range of block ids of start blocks for hashesin that range. This is useful when resizing a hash table or merging two hashtables together.
Interleaving status bytes and key ids#
Status bytes and key ids for all slots are stored in a single array of bytes.They are first grouped by 8 into blocks, then each block of status bytes isinterleaved with a corresponding block of key ids. Finally key ids arerepresented using the smallest possible number of bits and bit-packed (bitsrepresenting each next key id start right after the last bit of the previous keyid). Note that regardless of the chosen number of bits, a block of bit-packedkey ids (that is 8 of them) will start and end on the byte boundary.
The diagram below shows the organization of bytes and bits of a single block ininterleaved array:
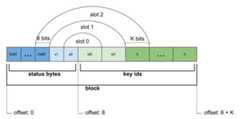
From the size of the hash table we can derive the number K of bits needed in theworst case to encode any key id. K is equal to the number of bits needed torepresent slot id (number of keys is not greater than the number of slots and anykey id is strictly less than the number of keys), which for a hash table of sizeN (N blocks) equals (N+3). To simplify bit packing and unpacking and avoidhandling of special cases, we will round up K to full bytes for K > 24 bits.
Status bytes are stored in a single 64-bit word in reverse byte order (the lastbyte corresponds to the slot with local id 0). On the other hand key ids arestored in the normal order (the order of slot ids).
Since both status byte and key id for a given slot are stored in the same arrayclose to each other, we can expect that most of the lookups will read only oneCPU cache-line from memory inside Swiss table code (then at least another oneoutside Swiss table to access the bytes of the key for the purpose ofcomparison). Even if we hit an overflow entry, it is still likely to reside onthe same cache-line as the start block data. Hash values, which are storedseparately from status byte and key id, are only used when resizing and do notimpact the lookups outside these events.
Note
Improvement to consider:In addition to the Swiss table data, we need to store an array of insertedkeys, one for each key id. If keys are of fixed length, then the address ofthe bytes of the key can be calculated by multiplying key id by the commonlength of the key. If keys are of varying length, then there will be anadditional array with an offset of each key within the array of concatenatedbytes of keys. That means that any key comparison during lookup will involve3 arrays: one to get key id, one to get key offset and final one with bytes ofthe key. This could be reduced to 2 array lookups if we stored key offsetinstead of key id interleaved with slot status bytes. Offset indexed by key idand stored in its own array becomes offset indexed by slot id and storedinterleaved with slot status bytes. At the same time key id indexed by slot idand interleaved with slot status bytes before becomes key id referenced usingoffset and stored with key bytes. There may be a slight increase in the totalsize of memory needed by the hash table, equal to the difference in the numberof bits used to store offset and those used to store key id, multiplied by thenumber of slots, but that should be a small fraction of the total size.
32-bit hash vs 64-bit hash#
Currently we use 32-bit hash values in Swiss table code and 32-bit integers askey ids. For the robust implementation, sooner or later we will need to support64-bit hash and 64-bit key ids. When we use 32-bit hash, it means that we runout of hash bits when hash table size N is greater than 25 (25 bits of hashneeded to select a block and 7 bits needed to generate a stamp byte reach 32total bits). When the number of inserted keys exceeds the maximal number of keysstored in a hash table of size 25 (which is at least\(2^{24}\)), the chanceof false positives during lookups will start quickly growing. 32-bit hash shouldnot be used with more than about 16 million inserted keys.
Low memory footprint and low chance of hash collisions#
Swiss table is a good choice of a hash table for modern hardware, because itcombines lookups that can take advantage of special CPU instructions with spaceefficiency and low chance of hash collisions.
Space efficiency is important for performance, because the cost of random arrayaccesses, often dominating the lookup cost for larger hash tables, increases withthe size of the arrays. This happens due to limited space of CPU caches. Let uslook at what is the amortized additional storage cost for a key in a hash tableapart from the essential cost of storing data of all those keys. Furthermore, wecan skip the storage of hash values, since these are only used during infrequenthash table resize operations (should not have a big impact on CPU cache usage innormal cases).
Half full hash table of size N will use 2 status bytes per inserted key (becausefor every filled slot there is one empty slot) and 2*(N+3) bits for key id(again, one for the occupied slot and one for the empty). For N = 16 forinstance this is slightly under 7 bytes per inserted key.
Swiss table also has a low probability of false positives leading to wasted keycomparisons. Here is some rationale behind why this should be the case. Hashtable of size N can contain up to\(2^{N+3}\) keys. Search for a matchinvolves (N + 7) hash bits: N to select a start block and 7 to use as a stamp.There are always at least 16 times more combinations of used hash bits thanthere are keys in the hash table (32 times more if the hash table is half full).These numbers mean that the probability of false positives resulting from asearch for a matching slot should be low. That corresponds to an expected numberof comparisons per lookup being close to 1 for keys already present and 0 fornew keys.
Lookup#
Lookup-or-insert operation, given a hash of a key, finds a list of candidateslots with corresponding keys that are likely to be equal to the input key. Thelist may be empty, which means that the key does not exist yet in the hashtable. If it is not empty, then the callback function for key comparison iscalled for each next candidate to verify that there is indeed a match. Falsepositives get rejected and we end up either finding an actual match or an emptyslot, which means that the key is new to the hash table. New keys get assignednext available integers as key ids, and are appended to the set of keys stored inthe hash table. As a result of inserting new keys to the hash table, the densityof occupied slots may reach an upper limit, at which point the hash table will beresized and will afterwards have twice as many slots. That is in summarylookup-or-insert functionality, but the actual implementation is a bit moreinvolved, because of vectorization of the processing and various optimizationsfor common cases.
Search within a single block#
There are three possible cases that can occur when searching for a match for agiven key (that is, for a given stamp of a key) within a single block,illustrated below.
There is a matching stamp in the block of status bytes:

There is no matching stamp in the block, but there is an empty slot in theblock:

There is no matching stamp in the block and the block is full (there are noempty slots left):

64-bit arithmetic can be used to search for a matching slot within the entiresingle block at once, without iterating over all slots in it. Following is anexample of a sequence of steps to find the first status byte for a given stamp,returning the first empty slot on miss if the block is not full or 8 (one pastmaximum local slot id) otherwise.
Following is a sketch of the possible steps to execute when searching for thematching stamp in a single block.
[1 instruction] Replicate stamp to all bytes by multiplying it by 0x 0101 01010101 0101.
We obtain: 0x 5E5E 5E5E 5E5E 5E5E.[1 instruction] XOR replicated stamp with status bytes word. Bytes correspondingto a matching stamp will be 0, bytes corresponding to empty slots will have avalue between 128 and 255, bytes corresponding to non-matching non-empty slotswill have a value between 1 and 127.
We obtain: 0x 1549 0064 0075 4FDE.[2 instructions] In the next step we want to have information about a match inthe highest bit of each byte. We can ignore here empty slot bytes, because theywill be taken care of at a later step. Set the highest bit in each byte (OR with0x 8080 8080 8080 8080) and then subtract 1 from each byte (subtract 0x 0101 01010101 0101 from 64-bit word). Now if a byte corresponds to a non-empty slot thenthe highest bit 0 indicates a match and 1 indicates a miss.
We obtain: 0x 95C9 80E4 80F5 CFDE,then 0x 94C8 7FE3 7FF4 CEDD.[3 instructions] In the next step we want to obtain in each byte one of twovalues: 0x80 if it is either an empty slot or a match, 0x00 otherwise. We doit in three steps: NOT the result of the previous step to change the meaningof the highest bit; OR with the original status word to set highest bit in abyte to 1 for empty slots; mask out everything other than the highest bits inall bytes (AND with 0x 8080 8080 8080 8080).
We obtain: 6B37 801C 800B 3122,then 6B37 DE3E DE2B 31A2,finally 0x0000 8000 8000 0080.[2 instructions] Finally, use leading zero bits count and divide it by 8 tofind an index of the last byte that corresponds either to a match or an emptyslot. If the leading zero count intrinsic returns 64 for a 64-bit input zero,then after dividing by 8 we will also get the desired answer in case of a fullblock without any matches.
We obtain: 16,then 2 (index of the first slot within the block that matches the stamp).
If SIMD instructions with 64-bit lanes are available, multiple single blocksearches for different keys can be executed together. For instance AVX2instruction set allows to process quadruplets of 64-bit values in a singleinstruction, four searches at once.
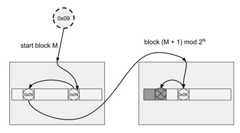
Complete search potentially across multiple blocks#
Full implementation of a search for a matching key may involve visiting multipleblocks beginning with the start block selected based on the hash of the key. Wemove to the next block modulo the number of blocks, whenever we do not find amatch in the current block and the current block is full. The search may alsoinvolve visiting one or more slots in each block. Visiting in this case meanscalling a comparison callback to verify the match whenever a slot with a matchingstamp is encountered. Eventually the search stops when either:
the matching key is found in one of the slots matching the stamp, or
an empty slot is reached. This is illustrated in the diagram below:
Optimistic processing with two passes#
Hash table lookups may have high cost in the pessimistic case, when we encountercases of hash collisions and full blocks that lead to visiting further blocks. Inthe majority of cases we can expect an optimistic situation - the start block isnot full, so we will only visit this one block, and all stamps in the block aredifferent, so we will need at most one comparison to find a match. We can expectabout 90% of the key lookups for an existing key to go through the optimisticpath of processing. For that reason it pays off to optimize especially for this90% of inputs.
Lookups in Swiss table are split into two passes over an input batch of keys. Thefirst pass: fast-path lookup, is a highly optimized, vectorized,SIMD-friendly, branch-free code that fully handles optimistic cases. Thesecondpass: slow-path lookup, is normally executed only for the selection of inputsthat have not been finished in the first pass, although it can also be calleddirectly on all of the inputs, skipping fast-path lookup. It handles all specialcases and inserts but in order to be robust it is not as efficient as fast-path.Slow-path lookup does not need to repeat the work done in fast-path lookup - itcan use the state reached at the end of fast-path lookup as a starting point.
Fast-path lookup implements search only for the first stamp match and only withinthe start block. It only makes sense when we already have at least one keyinserted into the hash table, since it does not handle inserts. It takes a vectorof key hashes as an input and based on it outputs three pieces of information foreach key:
Key id corresponding to the slot in which a matching stamp was found. Any validkey id if a matching stamp was not found.
A flag indicating if a match was found or not.
Slot id of a slot from which slow-path should pick up the search if the firstmatch was either not found or it turns out to be false positive afterevaluating key comparison.
Note
Improvement to consider: precomputing 1st pass lookup results.
If the hash table is small, the number of inserted keys is small, we couldfurther simplify and speed-up the first pass by storing in a lookup tablepre-computed results for all combinations of hash bits. Let us consider thecase of Swiss table of size 5 that has 256 slots and up to 128 inserted keys.Only 12 bits of hash are used by lookup in that case: 5 to select a block, 7to create a stamp. For all\(2^{12}\) combinations of those bits we couldkeep the result of first pass lookup in an array. Key id and a matchindicating flag can use one byte: 7 bits for key id and 1 bit for the flag.Note that slot id is only needed if we go into 2nd pass lookup, so it can bestored separately and likely only accessed by a small subset of keys.Fast-path lookup becomes almost a single fetch of result from a 4KB array.Lookup arrays used to implement this need to be kept in sync with the maincopy of data about slots, which requires extra care during inserts. Since thenumber of entries in lookup arrays is much higher than the number of slots,this technique only makes sense for small hash tables.
Dense comparisons#
If there is at least one key inserted into a hash table, then every slot containsa key id value that corresponds to some actual key that can be used incomparison. That is because empty slots are initialized with 0 as their key id.After the fast-path lookup we get a match-found flag for each input. If it isset, then we need to run a comparison of the input key with the key in the hashtable identified by key id returned by fast-path code. The comparison will verifythat there is a true match between the keys. We only need to do this for asubset of inputs that have a match candidate, but since we have key id valuescorresponding to some real key for all inputs, we may as well executecomparisons on all inputs unconditionally. If the majority (e.g. more than 80%)of the keys have a match candidate, the cost of evaluating comparison for theremaining fraction of keys but without filtering may actually be cheaper than thecost of running evaluation only for required keys while referencing filterinformation. This can be seen as a variant of general preconditioning techniquesused to avoid diverging conditional branches in the code. It may be used, basedon some heuristic, to verify matches reported by fast-path lookups and isreferred to asdense comparisons.
Resizing#
New hash table is initialized as empty and has only a single block with a spacefor only a few key entries. Doubling of the hash table size becomes necessary asmore keys get inserted. It is invoked during the 2nd pass of the lookups, whichalso handles inserts. It happens immediately after the number of inserted keysreaches a specific upper limit decided based on a current size of the hash table.There may still be unprocessed entries from the input mini-batch after resizing,so the 2nd pass of the lookup is restarted right after, with the bigger hashtable and the remaining subset of unprocessed entries.
Current policy, that should work reasonably well, is to resize a small hash table(up to 8KB) when it is 50% full. Larger hash tables are resized when 75% full.We want to keep size in memory as small as possible, while maintaining a lowprobability of blocks becoming full.
When discussing resizing we will be talking aboutresize source andresizetarget tables. The diagram below shows how the same hash bits are interpreteddifferently by the source and the target.

For a given hash, if a start block id was L in the source table, it will beeither (2*L+0) or (2*L+1) in the target table. Based on that we can expect dataaccess locality when migrating the data between the tables.
Resizing is cheap also thanks to the fact that hash values for keys in the hashtable are kept together with other slot data and do not need to be recomputed.That means that resizing procedure does not ever need to access the actual bytesof the key.
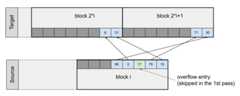
1st pass#
Based on the hash value for a given slot we can tell whether this slot containsan overflow or non-overflow entry. In the first pass we go over all source slotsin sequence, filter out overflow entries and move to the target table all otherentries. Non-overflow entries from a block L will be distributed between blocks(2*L+0) and (2*L+1) of the target table. None of these target blocks canoverflow, since they will be accommodating at most 8 input entries during thispass.
For every non-overflow entry, the highest bit of a stamp in the source slotdecides whether it will go to the left or to the right target block. It isfurther possible to avoid any conditional branches in this partitioning code, sothat the result is friendly to the CPU execution pipeline.
2nd pass#
In the second pass of resizing, we scan all source slots again, this timefocusing only on the overflow entries that were all skipped in the 1st pass. Wesimply reinsert them in the target table using generic insertion code with oneexception. Since we know that all the source keys are different, there is noneed to search for a matching stamp or run key comparisons (or look at the keyvalues). We just need to find the first open block beginning with the startblock in the target table and use its first empty slot as the insertdestination.
We expect overflow entries to be rare and therefore the relative cost of thatpass should stay low.

