Movatterモバイル変換
[0]ホーム
Segmentotopes
External
links |  |
In 2000 Klitzing published[1] on segmentotopes in general resp. hisresearch on convex segmentochora in special. Segmentotopes are polytopes which bow to the following conditions:
- all vertices on the surface of 1 hypersphere
- all vertices on 2 parallel hyperplanes
- all edges of 1 length
The first condition shows that the circumradius is well defined. Moreover, in union withcondition 3 this implies that all 2D faces have to be regular. The sandwich type 2nd condition implies that all edges,which aren't contained completely within one of the hyperplanes, would join both, i.e. having onevertex each in either plane. Thence segmentotopes have to be monostratic. In fact,segmentotopes are the monostraticorbiforms. (Orbiforms, a terminus which had been created several years later only, just use the first and third condition of those.)Finally it follows, that the bases have to be orbiforms, while all the lacing elements have to be (lower dimensional) segmentotpes.
The naming of individual segmentotopes usually is based on the 2 base polytopes: top-base polytopeatopbottom-base polytope. Symbolically one uses the parallelness of those bases: Ptop || Pbottom.(For the smaller segmentotopes the choice of bases need not be unique.)
Segmentotopes are closely related tolace prisms. In fact those concepts have a large common intersection,but they are not identical. While lace prisms need an axis of symmetry (in fact one which is describable as Dynkin symbol), one uses the terminus "axis" in the context of segmentotopes only in the sense of the line defined by the centers of the circumspheres of d-1 dimensional bases. (Thus the topic ofaxial polytopes does more relate to lace towers (asmultistratic generalizations of lace prisms) than to segmetotopes. None the less there is a large overlap.)– Note that the radius R of the d-1 dimensional circumsphere used for a segmentotpal base of dimension d-k might well be larger than the radiusr of its d-k dimensional circumsphere: for k > 1 the latter might well be placed within the former with some additional shifts: R2 = r2 + s2. For a simple example just considersquippy, the 4-fold pyramid,which is just half of anoct, when being considered asline ||triangle: the subdimensional base,the single edge, there is placed off-set.
In fact, letrk be the individual circumradii of the bases, letsk be the respective shifts away from the axis(if subdimensional), leth be the axial height andR the global circumradius, then we have the following interrelation formulabetween all these sizes 4 R2 h2 = ((r22+s22)-(r12+s12))2 + 2 ((r12+s12)+(r22+s22)) h2 + h4.
Convex Segmentochora (up)
Just as polytopes are distinguished dimensionally as polygons, polyhedra, polychora, etc.so too are segmentotopes.
The onlysegmentogons (without any further adjectivic restriction) clearly are
- regular triangle (point ||line) and
- square (line ||line).
Segmentohedra already include infinite series like
(*) Grünbaumian bottom base understood to be withdrawn.
For convex ones d clearly has to be 1 and several of the above series then become finite.
Polychora generally have the disadvantage not being visually accessible.Segmentochora are not so hard for that:Just consider the 2 base polyhedra displayed concentrically, perhaps slightly scaled, while the lacings thenget slightly deformed. Mathematically speaking, axial projections (view-point at infinity) and central projections (finite view-point),either one being taken on the axis for sure, from 4D onto 3D generally are well "viewable" for such monostratic figures. Especially when using real 3D graphics (like the here used VRMLs) instead of further projections onto 2D as in usual pictures: Note that all pictures at "segmentochoron display" within individual polychoron files will be linked to such VRML files.
Color coding of the following pictures:
| fore color | back color | explanation |
red | - | Ptop |
blue | - | Pbottom |
gold | - | lacing edges |
| - | white | spherical geometry |
| - | light yellow | euclidean geometry – cf. also:decompositions |
| - | light green | hyperbolic geometry |
Cases with Tetrahedral Axis:

Cases with Octahedral Axis:

Cases with Icosahedral Axis:
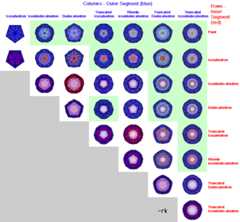
Cases with n-Prismatic or n-Antiprismatic Axis:
Non-Lace-Prismatics:
Just as already often was used within the set ofJohnson solids, several of the above segmentochora allowdiminishings too. Those generally break some symmetries of one or both bases, and therefore too of the axial symmetry.Thus there is no longer a unifying symmetry according to which aDynkin symbol could be designed,being the premise for lace prisms.Even though, such diminished ones are fully valid segmentotopes (following the above 3 conditions). An easy 3D example could be againline ||triangle,the alternate description of the above mentionedsquippy. The easiest 4D one clearly issquasc (i.e. the 1/4-lune of thehex).–Gyrations in some spare cases might apply as well,although those in general would conflict to the requirement of exactly 2 vertex layers.
But there is also a generic non-lace-prismatic convex segmentochoron with octahedral symmetry at one base,with icosahedral symmetry at the other. (The common subsymmetry clearly is the pyrital. But that one does not bow to Dynkin symbol description.)That one uses as faces 1cube (as bottom base), 6trip (asline ||square), 12squippy (astriangle ||line),8tet (astriangle ||point), and1ike (as top base).

Full Table:
(For degenerate segmentochora, i.e. having zero heights, cf. page "finite flat complexes".)
Close Relatives:
In 2012 two sets of closely related monostratic polytopes where found:
In fact the constraint, of the lacing edges all having unit lengths too, results in some specific shift values for the base polyhedra.As those base polyhedra on the other hand are not degenerate, this conflicts to having a common circumsphere in general: within thecase of pyramids only the special value n=3 results in a true convex segmentochoron (being thehex), within thecase of cupolae only the special value n=2 results in a true convex segmentochoron (beingtrip || refl ortho trip).Even though, the values n=3,4,5 resp. n=2,3,4,5 would well generate monostratic convex regular-faced polychora (CRFs).
The closeness even could be pushed on a bit. If one of the (equivalent) bases each, which are segmentohedra in turn, would be diminished by omitting the smaller top face, i.e. maintaining therefrom only the larger bottom face, those would re-enter the range of valid segmentochora again:{n} || gyro n-py resp.{2n} || n-cu. In fact, here the necessary shifts of the bases could be assembled at the degenerate base alone. There a non-zero shift is known to be allowed.
Without narrowing those findings, those 2 families could be de-mystified a bit by using different axes: the pyramidal case is nothing but the bipyramid of the n-antiprism, while the cupolaic case is nothing but the bistratic lace towerxxo-n-oxx oxo&#xt.
Later the author realised also the existance of their ortho counterparts:
Again those can be splitted at their now always prismatic pseudofacial equatorFor the pyramidal ones, the case n=2 becomes subdimensional, there representing nothing but theoct.The general case here is nothing but the n-prismatic bipyramid.For the cupolaic case N=2 clearly is full dimensional, but pairs of containedsquippies becomecorealmic and thus unite intoocts. Therefore that case happens to become nothing butope.
In 2014 three close relatives to pyramids have been found, which are not orbiform just because their base is not. Those areline || bilbiro,{3} || thawro, resp.{5} || pocuro. A further such case would beline || esquidpy.
Besides of considering 2 parallel hyperplanes cutting out monostratic layers of larger polychora, in 2012 (and more deeply in 2013) considerations about 2 intersecting equatorial hyperplanes were done. Those clearly cut out wedges. The specific choice of those hyperplanesmade up the terminuslunae. Only theCRF ones were considered. The followinglunae are known so far:
- Lunae ofhex: cells beingsquippy andtet
- 1/4-luna ofhex =squasc = pt ||squippy(thus a segmentochoron) – hyperplanes intersect at 90°.
- Lunae ofico: cells beingtricu,oct, andsquippy
- Lunae ofex: cells beingpero,peppy, andtet
- Lunae ofspid resp.gyspid: cells beingtricu,tet, andtrip
- 0.290215-luna ofspid =tet || tricu(thus a segmentochoron) – hyperplanes intersect at arccos(-1/4) = 104.477512°.
- 0.209785-luna ofspid ={3} || tricu(thus a segmentochoron) – hyperplanes intersect at arccos(1/4) = 75.522488°.
- 0.419569-luna ofgyspid ={3} || tricu || {3}– hyperplanes intersect at 2 arccos(1/4) = arccos(-7/8) = 151.044976°.
- Lunae ofquawros: cells beingsquacu,cube,tet, andtrip
- Lunae ofstawros: cells beingpecu,pip,tet, andtrip
- Surely the convexity restriction could be released. Some3D examples can be found on the page onaxials.
Some4D cases would be e.g.- 0.591923 -gissidpy = pt || gissid =oo3oo5/2ox&#x
- 0.613502 -quithpy = pt || quith =oo3ox4/3ox&#x
- 0.618034 -gikepy = pt || gike =ox3oo5/2oo&#x
- 0.618034 -sissidpy = pt || sissid =ox5/2oo5oo&#x
- 0.618034 -stasc = line || perp {5/2} =xo ox5/2oo&#x
- 0.618034 -gissidragike = narrower gissid || gike =ox3oo5/3xo&#x
- 0.618034 -shallower gissidasissid = gissid || sissid (with lacing starps)
- 0.621876 -ogasc = line || perp {8/3} =xo ox4/3ox&#x
- 0.658240 -shasc = line || perp {7/2} =xo ox7/2oo&#x
- 0.662791 -gissidagike = taller gissid || gike =ox3oo5/2xo&#x
- 0.662791 -taller gissidasissid = gissid || sissid (with lacing staps)
- 0.662791 -stapepy = point || stap =oxo5/2oox&#x
- 0.692924 -gissidagid = gissid || gid =oo3ox5/2xo&#x
- 0.726543 -gikagid = gike || gid =xo3ox5/2oo&#x
- 0.707107 -hossdap = pseudo sissid || pseudo sissid =reduced( β2β5o5/2o , by β5o5/2o )
- 0.707107 -starpglassit = stappy || inv stappy =xooo5/2ooxo&#xr
- 0.707107 -tho = tet || dual pseudo tet =hemi( x3o3/2o3o3*a )
- 0.707107 -fitetaltet = faceted tet || dual tet =reduced( xx3/2ox3oo&#x , by x3/2x )
- 0.739539 -quith || "thah-squares star" =reduced( xo4/3xx3/2ox&#x , by oct )
- 0.774597 -tutrippapy = pt || tutrip =reduced( oox4/2oxx&#x , by ..x4/2..x )
- 0.774597 -tubidrap = pseudo {4} || so =reduced( oxx4/2xox&#x , by ..x4/2..x )
- 0.774597 -firp = tet || pseudo 2thah =reduced( xx3/2oo3ox&#x , by x3/2o3x )
- 0.774597 -fitetaoct = faceted 3tet || oct =reduced( ox3/2xx3oo&#x , by x3/2x )
- 0.774597 -hotetahoct = pseudo tet || pseudo oct =reduced( xx3/2ox3oo3*a&#x , by x3/2x )
- 0.774597 -pafirp = tet || "thah-squares star" =reduced( xx3/2xo3ox&#x , by x3/2x )
- 0.774597 -{3} || pseudo gyro trip =reduced( ox xx3/2ox&#x , by x3/2x )
- 0.780850 -tistadip = {5/2} || stip =x3o x5/2o
- 0.790569 -tutepe = pseudo {4} || {4/2}-prism =reduced( ox xo4/2xx&#x , by x.4/2x. )
- 0.791345 -tistodip = {8/3} || stop =x3o x8/3o
- 0.825168 -stappip = stap || stap =x s2s5/2s = narrower stip || stip =xx xo5/2ox&#x
- 0.866025 -"coord-axes edge star" || cube
- 0.874032 -stacupe = stip || 2pip =xx5/2ox&#x
- 0.874032 -quit sissidagird = quit sissid || gird =reduced( ox5/4xx5/3xx&#x , by x5/4x )
- 0.879465 -"thah-squares star" || cube
- 0.881132 -sistadip = stip || stip =x4o x5/2o
- 0.890446 -cubaquerco = cube || querco =ox3/2oo4xx&#x
- 0.890446 -sistodip = stop || stop =x4o x8/3o
- 0.912871 -"coord-planes square star" || cube
- 0.951057 -sidtidap = sidtid || gyro sidtid =xo5/2ox3oo3*a&#x
- 0.951057 -gidtidap = gidtid || gyro gidtid =xo5/4ox3oo3*a&#x
- 0.951057 -ditdidap = ditdid || gyro ditdid (the blend of the latter 2)
- 1 -sidtidpy = pt || sidtid =xo3oo3oo5/2*b&#x
- 1 -gidtidpy = pt || gidtid =xo3oo3/2oo5*b&#x
- 1 -ditdidpy = pt || ditdid =xo5oo3/2oo5/2*b&#x
- 1 -tetacho = tet || cho =reduced( ox3/2ox3xx&#x , by x3/2x )
- 1 -hotet aoho = pseudo 2tet || oho =reduced( xx3/2oo3ox3*a&#x , by x.3/2o.3o.3*a )
- 1 -sissidagad = sissid || gad =xo5/2oo5ox&#x
- 1 -co retro-cuploid = "thah-squares star" || co =reduced( ox3/2xx4oo&#x, by .x3/2.x4.o )
- 1 -hoctaoho = pseudo 2oct || oho =reduced( xx3/2xo3ox3*a&#x, by x.3/2x.3o.3*a )
- 1 -octacho = oct || cho =reduced( ox3/2xx3ox&#x, by x3/2x )
- 1 -hothahacho = pseudo thah || cho =reduced( xx3/2ox3xx&&#x, by x3/2x )
- 1 -gikaike = gike || ike
- 1 -sirgikaike (edge-faceting ofgikaike)
- 1 -girgikaike (edge-faceting ofgikaike)
- 1 -cubagike = cube || gike
- 1.064815 -gaddadid = gad || did =xo5ox5/2oo&#x
- 1.064815 -sissidadid = sissid || did =oo5ox5/2xo&#x
- 1.082392 -quithaquitco = quith || quitco =ox3xx4/3xx&#x
- 1.120533 -tiggia gaquatid = tiggy || gaquatid =xx3xx5/3ox&#x
- 1.136572 -gidtidagiid = gidtid || giid =oo3/2ox3xx5*a&#x
- 1.183216 -ohoa hotut = oho || pseudo 2tut =reduced( xx3/2xo3xx3*a&#x, by x.3/2x.3o.3*a )
- 1.183216 -choatut = cho || tut =reduced( ox3/2xx3xx&#x, by x3/2x )
- 1.328131 -gaddaraded = gad || raded =xx5oo5/2ox&#x
- 1.336349 -dida raded = raded || tigid =xx5ox5/2xo&#x
- 1.414214 -didadoe = did || doe =reduced( oo5xx5/2ox&#x, by x5/2x )
- 1.414214 -goccoa cotco = gocco || cotco =xx3ox4xx4/3*a&#x
- 1.432173 -radedadoe = raded || doe =reduced( ox5xo5/2xx&#x , by x5/2x )
- 1.618034 -gadadoe = gad || doe
- 1.765796 -siida = siid || gyro siid =xo5/2ox3xx3*a&#x
- 2.363565 -radeda tigid = did || tigid =ox5xx5/2oo&#x
- 2.497212 -sissidaraded = sissid || raded =ox5oo5/2xx&#x
- 3.835128 -sidtidasiid = sidtid || siid =xx5/2oo3ox3*a&#x
- 4.352502 -diddatigid = did || tigid =ox5xx5/2oo&#x
- 4.684471 -gidditdid aidtid = gidditdid || idtid =xx5/3xx3ox5*a&#x
- ... -n/d scalene = line || perp {n/d} =xo ox-n/d-oo&#x
- ...
- By means of externalblends at the bases multistratic stacks can be derived, right in the sense oflace towers. But in general,orbiformitythereby is lost. Only few are known, which then still are. Among those clearly are the ones which can be deduced asmultistratic segments of uniform or evenscaliform polytopes. But there arealso rare exceptional finds beyond those, e.g.
- sidrebcu = sissid || (pseudo) did || gad =xoo5/2oxo5oox&#xt
- ...
Further Reading
- ↑ Convex Segmentochora –(PDF)
published as: "Convex Segmentochora", by Dr. R. Klitzing,Symmetry: Culture and Science, vol. 11, 139-181, 2000 - externallink (hosted by J. McNeill)
---- 5D----
(Just some) Convex Segmentotera (up)
| | Circumradius | Segmentoteron |
|---|
| 1.322876 | hacube = shiddip || shiddip (uniform)rittip = rit || rit (uniform)tutcupip = tuttip || inv tuttip (segment ofrittip)= tuta || tutatepeatuttip = tepe || tuttip (segment ofrittip)= tetatut || tetatut | | 1.360147 | tippip = tip || tip (uniform) | | 1.369306 | squatut = tuttip || tuttip (uniform) | | 1.414214 | pennatip = pen || tip (segment ofrin)tipadeca = tip || deca (segment ofrin)octatuttip = oct || tuttip (segment ofsibrid)sripadeca = srip || deca (half ofsibrid)hatricu = thiddip || hiddip (half ofhaco) | | 1.442951 | otet = {8} || todip (uniform)= op || lacing-ortho op | | 1.462497 | trasnic = snic || sniccup (uniform) | | 1.485633 | owoct = todip || {3}-gyro todip (uniform) | | 1.5 | decap = deca || deca (uniform) | | 1.502958 | rita sidpith = rit || sidpithsirco acope = sirco || cope | | 1.513420 | trasirco = sirco || sircope (uniform) | | 1.515539 | tradoe = doe || dope (uniform) | | 1.518409 | squasnic = sniccup || sniccup (uniform) | | 1.567516 | ocube = sodip || sodip (uniform)squasirco = sircope || sircope (uniform)sidpithip = sidpith || sidpith (uniform, segment ofscant)squicuffip = squicuf || squicuf (wedge ofsidpithip)= tes || op | | 1.569562 | squadoe = dope || dope (uniform) | | 1.583946 | toa sircope = toe || sircope | | 1.618035 | idadope = id || dope | | 1.620185 | ritag thex = rit || gyro thex (segment ofsirhin)thexa = thex || gyro thex (scaliform, segment ofsirhin)teta tuttip = tet || tuttip (segment ofsirhin)rapadeca = rap || deca (segment ofsirhin)deca aprip = deca || prip (segment ofsirhin)tutcupa toe = tuta || toe (wedge ofsirhin) | | 1.632993 | tipalprip = tip || inv prip (segment ofcappix)tuttipa toe = tuttip || toe (wedge ofcappix) | | 1.658312 | triddippa hiddip = trddip || hiddip (segment ofcard)pripa = prip || inv prip (segment ofcard)sripaprip = srip || prip (segment ofcard)thexip = thex || thex (uniform) | | 1.683251 | tratoe = toe || tope (uniform) | | 1.688194 | prippip = prip || prip (uniform)tuttipa tope = tuttip || tope (segment ofprippip) = tutatoe || tutatoe | | 1.693527 | exip = ex || ex (uniform)gappip = gap || gap (uniform)sadip = sadi || sadi (uniform) | | 1.695040 | cuba sircope = cube || sircope | | 1.717954 | trid = id || iddip (uniform) | | 1.719624 | haop = hodip || hodip (uniform) | | 1.732051 | squatoe = tope || tope (uniform)icathex = ico || thex (segment ofsart)thexarico = thex || rico (segment ofsart)sripalprip = srip || inv prip (segment ofsart)trashiddip = {3} || shiddip (segment ofsart)cotut totric = co || tutatoe (wedge ofsart)= coatut || toe= tut || coatoe | | 1.738546 | ricoasadi = rico || sadidoa iddip = doe || iddip | | 1.765796 | squid = iddip || iddip (uniform) | | 1.778824 | ricoa = rico || gyro rico (scaliform) | | 1.802776 | ricope = rico || rico (uniform)copatope = cope || tope (segment ofricope) = coatoe || coatoe | | 1.847759 | coasircope = co || sircopeica sidpith = ico || sidpithricasrit = rico || sritricoaspic = rico || spic | | 1.848423 | pripalgrip = prip || gyro grip (segment ofpattix)tutatope = tut || tope (segment ofpattix) | | 1.870173 | tratic = tic || ticcup (uniform) | | 1.870829 | ritarico = rit || rico (segment ofspat)spidaprip = spid || prip (segment ofspat)pripagrip = prip || grip (segment ofspat)gripa = grip || inv grip (segment ofspat)copatoe = cope || toe (wedge ofspat) | | 1.910497 | grippip = grip || grip (uniform) | | 1.914214 | ticca sircope = tic || sircopesquatic = ticcup || ticcup (uniform)spiccup = spic || spic (uniform)srittip = srit || srit (uniform, segment ofspan)sidpith || srit (segment ofspan) | | 1.914854 | deca agrip = deca || grip (segment ofpirx) | | 1.994779 | cuba octu = cube || octu | | 2.117085 | twacube = sitwadip || sitwadip (uniform) | | 2.150581 | taha = tah || gyro tah (scaliform, segment ofpirhin)tipagrip = tip || grip | | 2.179449 | tahp = tah || tah (uniform) | | 2.207107 | tattip = tat || tat (uniform)srit || tat (segment ofsirn)rap || tip (segment ofsirn)sircoa ticcup = sirco || ticcup (segment ofsirn){4} || todip (segment ofsirn) | | 2.231808 | trasnid = snid || sniddip (uniform) | | 2.236068 | ricatah = rico || tah (segment ofsibrant)sripagrip = srip || grip (segment ofsibrant)coatope = co || tope (wedge ofsibrant) | | 2.268840 | squasnid = sniddip || sniddip (uniform) | | 2.291288 | gippiddip = gippid || gippid (uniform) | | 2.306383 | trasrid = srid || sriddip (uniform) | | 2.327373 | gripagippid = grip || gippid (segment ofcograx) | | 2.342236 | squasrid = sriddip || sriddip (uniform) | | 2.371708 | thexagtah = thex || gyro tah | | 2.388442 | tragirco = girco || gircope (uniform) | | 2.423081 | squagirco = gircope || gircope (uniform)prittip = prit || prit (uniform) | | 2.544388 | trati = ti || tipe (uniform) | | 2.576932 | squati = tipe || tipe (uniform) | | 2.632865 | ritasrit = rita || sritsricoa = srico || gyro srico (scaliform)prohalsrico = proh || gyro srico (diminishing ofsricoa) | | 2.647378 | tico || prissi | | 2.660531 | prohp = proh || proh (uniform, segment ofcarnit)prit || proh (segment ofcarnit)prit || srit (segment ofcarnit)hodip || tisdip (segment ofcarnit)sricope = srico || srico (uniform) | | 2.692582 | ticope = tico || tico (uniform) | | 2.738613 | pripa gippid = prip || gippid (segment ofpattit) | | 2.878460 | proh || tat (segment ofcapt) | | 3 | tahatico = tah || tico (segment ofpirt) | | 3.025056 | tratid = tid || tiddip (uniform) | | 3.047217 | grittip = grit || grit (segment ofprin) | | 3.052479 | squatid = tiddip || tiddip (uniform) | | 3.118034 | roxip = rox || rox (uniform) | | 3.239235 | prohagrit = proh || grit (segment ofpattin)ticca gircope = tic || gircope | | 3.450631 | contip = cont || cont (uniform) | | 3.522336 | pricoa = prico || gyro prico (scaliform) | | 3.534493 | pricope = prico || prico (uniform)gidpithip = gidpith || gidpith (uniform, segment ofcogart) | | 3.736068 | hipe = hi || hi (uniform) | | 3.845977 | tragrid = grid || griddip (uniform) | | 3.867584 | squagrid = griddip || griddip (uniform) | | 3.988340 | gritta gidpith = grit || gidpith (segment ofcogrin) | | 4.311477 | gricoa = grico || gyro grico (scaliform) | | 4.328427 | gricope = grico || grico (uniform) | | 4.562051 | rahipe = rahi || rahi (uniform) | | 4.670365 | thipe = thi || thi (uniform) | | 4.749980 | texip = tex || tex (uniform) | | 4.776223 | grixip = grix || grix (uniform) | | 5.194028 | gippiccup = gippic || gippic (uniform) | | 5.259887 | sidpixhip = sidpixhi || sidpixhi (uniform) | | 6.094140 | srixip = srix || srix (uniform) | | 6.753568 | srahip = srahi || srahi (uniform) | | 7.596108 | xhip = xhi || xhi (uniform) | | 8.294035 | prahip = prahi || prahi (uniform) | | 9.757429 | prixip = prix || prix (uniform) | | 11.263210 | grahip = grahi || grahi (uniform) | | 12.796423 | gidpixhip = gidpixhi || gidpixhi (uniform) | | ... | 3,n-dippip = n-p || 4,n-dip (uniform)= 3,n-dip || 3,n-dip | | ... | n,cube-dip = 4,n-dip || 4,n-dip (uniform) | | ... | n,m-dippip = n,m-dip || n,m-dip (uniform) | | ... | (n,m-ap)-dip = n,m-dip || para-gyro n,m-dip (uniform) | | ... | n,m-dafup = n,m-dip || bidual n,m-dip (scaliform) | | ... | n-daf = n-p || bidual n-p (scaliform) | | ... | (n, dual n, n-p)-tric = n-g || gyro 3,n-dip | | ... | (n, n-p, gyro n-p)-tric = n-g || n-appip |
|
(For degenerate segmentotera, i.e. having zero heights, cf. page "finite flat complexes".)
Somenon-convex segmentotera would be:
- 0.623054 -stadow = pentagram || fully perp. pentagram (aka: star disphenoid)
- 0.629640 -ogdow = octagram || fully perp. octagram (aka: octagram disphenoid)
- 0.633157 -quithesc = line || fully perp. quith (aka: quith scalene)
- 0.636010 -sissidisc = line || fully perp. sissid (aka: sissid scalene)
- 0.636010 -state = triangle || fully perp. pentagram (aka: star tettene)
- 0.636010 -gogishiragax = narrower gogishi || gax (aka: gogishi-gax retroprism)
- 0.638475 -togdow = triangle || fully perp. octagram (aka: triangle-octagram disphenoid)
- 0.667731 -gogishiagax = taller gogishi || gax (aka: gogishi-gax antiprism)
- 0.674163 -shadow = small heptagram || fully perp. small heptagram (aka: small heptagrammic disphenoid)
- 0.680827 -gashia = gashi || dual gashi (aka: gashi antiprism)
- 0.707107 -bostarpglassdit =oxo(-x) xooo5/2ooxo&#xr
- 0.707107 -hehad = pen || dual pseudo pen (aka: demicross)
- 0.707107 -phap = (non-convex) pen || dual pen (aka: pennic hemiantiprism)
- 0.707107 -nophap = pseudo pen || dual pseudo pen (aka: spinopennic hemiantiprism)
- 0.707107 -sistadow = square || fully perp. pentagram (aka: (square,star)-disphenoid)
- 0.816497 -firx = pen || firp
- 0.951057 -gadtaxhiap = gadtaxhi || alt. gadtaxhi (aka: gadtaxhi alterprism, uniform)
- 0.951057 -gadtaxadiap = gadtaxady || alt. gadtaxady (aka: gadtaxady alterprism)
- 1.050501 -gicalico = gico || dual ico (aka: blend of 3 icateses)
- 1.074481 -sishia = narrower sishi || sishi (aka: sishi alterprism)
- 1.125151 -pirgadia = pirgady || alt. pirgady (aka: pirgady alterprism)
- 1.209137 -traquitco = quitco || quitcope
- 1.248606 -ragashia = ragashi || inv ragashi (aka: ragashi alterprism)
- 1.618034 -sirgashia = sirgashi || inv sirgashi (aka: sirgashi alterprism)
- 1.666693 -sirgaship = sirgashi || sirgashi (aka: sirgashi prism)
- 1.677756 -sutia = suti || alt. suti (aka: suti alterprism)
- 1.693527 -gohip = gohi || gohi (aka: gohi prism, uniform)
- 1.917564 -righia = righi || inv righi (aka: righi alterprism)
- 2.321762 -sidtaxhiap = sidtaxhi || alt. sidtaxhi (aka: sidtaxhi alterprism, uniform)
- 2.321762 -sirdtaxadiap = sirdtaxady || alt. sirdtaxady (aka: sirdtaxady alterprism)
- 2.352869 -ditdia = ditdi || alt. ditdi (aka: ditdi alterprism)
- 2.527959 -sid pippadia = narrower sid pippady || sid pippady (aka: sid pippady alterprism)
- 2.829949 -rasishia = narrower rasishi || rasishi (aka: rasishi alterprism)
- 3.118034 -sophip = sophi || sophi (aka: sophi prism)
- 3.404434 -sirghia = sirghi || inv sirghi (aka: sirghi alterprism)
- 3.423760 -sirghipe = sirghi || sirghi (aka: sirghi prism)
- 3.855219 -stut phiddixa = stut phiddix || alt. stut phiddix (aka: stut phiddix alterprism)
- 4.923348 -pirghia = pirghi || inv pirghi (aka: pirghi alterprism)
- 5.345177 -wavhiddixa = wavhiddix || alt. wavhiddix (aka: wavhiddix alterprism)
- 6.893126 -sphiddixa = sphiddix || alt. sphiddix (aka: sphiddix alterprism)
---- 6D----
(Just some) Convex Segmentopeta (up)
| | Circumradius | Segmentopeton |
|---|
| 1 | dotip = dot || dot (uniform)= rappip || inv rappiptridafupip = tridafup || tridafup (segment ofdotip)= tratrip || bidual tratripsquahex = hexip || hexip (uniform)hixascad = hix || scad (segment ofstaf)spidapenp = spid || penp (segment ofstaf)hexippy = pt || hexip (segment ofrag)hexipaico = hexip || ico (wedge ofrag)hexipaco = hexip || co (wedge ofrag)taccarat = tac || rat (segment ofrag)hexarat = hex || rat (segment ofrag)rixascad = rix || scad (segment ofrag)dotpy = pt || dot (segment ofmo)dottascad = dot || scad (segment ofmo)hinro = hin || rat (segment ofmo)hinatedrat = hin || tedrat (segment ofmo)icoahin = ico || hin (segment ofmo)hinaco = hin || co (segment ofmo)penal rappip = pen || alt rappip (segment ofmo)spidarappip = spid || rappip (wedge ofmo)tetaopepy = pen || ope (wedge ofmo)= tet || opepy= pt || teta opehexaoctaco tettic = co || bidhin (wedge ofdottascad)= oct || hexaco= tet || alt. rapacotetaco altepetric = co || tetaf= tet || hexaco= tet || inv tepacotriddipasc = line || perp triddip | | 1.118034 | ratip = rat || rat (uniform)scadip = scad || scad (uniform) | | 1.123033 | icaf = ico || dual icope | | 1.195229 | rixalspix = rix || inv spix (segment ofscal)scadaspix = scad || spix (segment ofscal) | | 1.224745 | ax = pent || pent (regular)troctpy = pt || troct (segment ofbrag)dottaspix = dot || spix (segment ofbrag)spixa = spix || inv spix (segment ofbrag)ratanit = rat || nit (segment ofbrag)hexcopedaw = hex || axis-ortho cope (segment ofbrag)hexaicope = hex || icope (segment ofbrag)troctal traco = troct || inv. traco | | 1.228783 | pentanit = pent || nit | | 1.290994 | spixip = spix || spix (uniform)ritgyt = rit || gyro rita (scaliform, wedge ofrojak)ritahin = rit || hin (wedge ofrojak)hinanit = hin || nit (segment ofrojak)nitasiphin = nit || siphin (segment ofrojak)ratasiphin = rat || siphin (segment ofrojak)rixaspix = rix || spix (segment ofrojak)spixalsarx = spix || inv sarx (segment ofrojak)icarita = ico || rita (wedge ofrojak)hexaico alrittric = hex || alt. icarit (wedge ofrojak)= ico || hexalrit= rit || alt. hexaicorappippy = pt || rappip (segment ofrojak)sripaf = srip || srippip | | 1.316561 | trasrip = srip || srippip (uniform) | | 1.322876 | tettut = tut || tratut (uniform)hinasiphin = hin || siphin (segment ofsochax)siphina = siphin || alt. siphin (segment ofsochax)ritas = rita || alt. rita (segment ofsiphina) | | 1.362770 | rixatix = rix || tix (segment ofsril) | | 1.369306 | siphinnip = siphin || siphin (uniform) | | 1.384437 | sarxip = sarx || sarx (uniform) | | 1.414214 | tixip = tix || tix (uniform)nitarin = nit || rin (segment ofbrox)rixasarx = rix || sarx (segment ofbrox)sarxasibrid = sarx || sibrid (segment ofbrox) | | 1.418705 | pentarin = pent || rin | | 1.581139 | bittixa = bittix || inv bittix (scaliform) | | 1.614654 | open = {8} || otet (uniform) | | 1.632993 | thexgyt = thex || gyro thexa (scaliform, wedge ofhejak)hinarin = hin || rin (segment ofhejak) | | 1.658312 | cappixa = cappix || alt cappix (scaliform)sirhina = sirhin || alt sirhin (scaliform, segment ofsophax) | | 1.732051 | cardip = card || card (uniform, segment ofram)dottasibrid = dot || sibrid (segment ofram)sibridacard = sibrid || card (segment ofram)nitasirhin = nit || sirhin (segment ofram)sirhinasart = sirhin || sart (segment ofram) | | 1.936492 | thina = thin || alt thin (scaliform) segment ofsirhax)sirhinathin = sirhin || thin (segment ofsirhax) | | 2.160247 | tahgyt = tah || gyro taha (scaliform, wedge ofharjak)rinathin = rin || thin (segment ofharjak) | | 2.236068 | sartabittit = sart || bittit (segment ofsiborg)bittita sibrant = bittit || sibrant (segment ofsiborg) | | 2.345208 | squagippid = gippiddip || gippiddip (uniform) | | 3 | gocadip = gocad || gocad (uniform) | | 4.855004 | gacnetip = gacnet || gacnet (uniform) | | ... | (n,pen)-dip = {n} || (n,tet)-dip (uniform) | | ... | (n-g, dual n-g, para n-p, gyro n-p) lace simplex | | ... | (n,m)-dip || (n,m)-dafup |
|
Somenon-convex segmentopeta would be:
- 0.639069 -ogquithdow = octagram || fully perp. quith
- 0.639240 -stasissiddow = pentagram || fully perp. sissid
- 0.645976 -tiquithdow = triangle || fully perp. quith
- 0.707107 -guhsa = hix || dual pseudo hix
- 0.707107 -starpglassdit =oxoo5/2ooox xooo5/2ooxo&#xr
- 0.845154 -firl = hix || firx
---- 7D----
(Just some) Convex Segmentoexa (up)
| | Circumradius | Segmentoexon |
|---|
| 1 | he = bril || inv bril (uniform)tetdippy = pt || tetdip (segment ofhe)tetdippa octdip = tetdip || octdip (segment ofhe)trarapdafup = trarap || bi-alt. trarap (segment ofhe)trapen altralrap = trapen || bi-alt. trarapsquarat = ratip || ratip (uniform) diminishing ofbarz)tettepe = tetdip || tetdip (uniform)trarix = rix || rixip (uniform, wedge oflaq)haxpy = pt || hax (segment oflaq)haxarag = hax || rag (segment oflaq)jakamo = jak || mo (segment oflaq)hopalbril = hop || inv bril (segment oflaq)brilastaf = bril || staf (segment oflaq)taccuppy = pt || taccup (segment ofrez)garag = gee || rag (segment ofrez)rilastaf = ril || staf (segment ofrez)hopastaf = hop || staf (segment ofsuph diminishing oflaq)rixasc = line || perp rixrixaf = rix || inv rixiptrial trahex = {3} || inv trahextrahex aico = trahex || icoratahinnip = rat || hinnip | | 1.040833 | titridafup = trittip || bidual trittip (scaliform)rixap = rixip || inv rixip (scaliform) | | 1.052209 | brillip = bril || bril (uniform) | | 1.060660 | haxip = hax || hax (uniform) | | 1.118034 | tratratrip = trittip || trittip (uniform)stafip = staf || staf (uniform)hinnipa ratip = hinnip || ratip | | 1.154701 | trarat = rat || ratip (uniform) | | 1.224745 | trahexpy = pt || trahex (segment ofbarz)ragabrag = rag || brag (segment ofbarz)scala = scal || inv scal (scaliform, segment ofbarz) | | 1.322876 | hept = ax || ax (regular)brilalspil = bril || inv spil (segment ofsco)scala spil = scal || spil (segment ofsco)cubico = squico || squico (uniform, segment oflin)rojaka = rojak || alt. rojak (scaliform, segment oflin)haxabrag = hax || brag (segment oflin)haxa cytedbrag = hax || cytedbrag (segment oflin)moarojak = mo || rojak (segment oflin)bragasochax = brag || sochax (segment oflin)brilpy = pt || bril (segment oflin)hinaratip = hin || ratip (segment oflin)spila = spil || inv spil (scaliform) | | 1.384437 | rojakip = rojak || rojak (uniform) | | 1.414214 | trasarx = sarx || sarxip (uniform)bragabrox = brag || brox (segment ofsez)ragasochax = rag || sochax (segment ofranq)jakarojak = jak || rojak (segment ofranq)rojakatrim = rojak || trim (segment ofranq) | | 1.451600 | srillip = sril || sril (uniform) | | 1.457317 | ohix = {8} || open (uniform) | | 1.581139 | broxarax = brox || rax (segment ofbersa)sabrila = sabril || inv. sabril (scaliform) | | 1.658312 | jakatrim = jak || trim (segment ofstanq)hejaka = hejak || alt. hejak (segment ofstanq) | | 1.732051 | haxabrox = hax || brox (segment ofrolaq)broxa sophax = brox || sophax (segment ofrolaq)rojaka hejak = rojak || hejak (segment ofrolaq) | | 1.936492 | crala = cral || inv. cral (scaliform)shopjaka = shopjak || alt. shopjak (scaliform, segment ofbranq) | | 2.207940 | thaxa = thax || alt. thax (scaliform, segment ofsirhesa) | | 2.5 | hagippiddip = hagippid || hagippid (uniform) | | 3.774917 | gotafip = gotaf || gotaf (uniform) | | 6.264982 | gopamp = gopam || gopam (uniform) | | ... | n,n,n-tippip = n,n,n-tip || n,n,n-tip (uniform) | | ... | (n,m)-dafupap = (n,m)-dafup || lacing-ortho (n,m)-dafup (scaliform) |
|
Somenon-convex segmentoexa would be:
- 0.646447 -quithdow = quith || fully perp. quith (aka: quith disphenoid)
- 0.831254 -sissiddow = sissid || fully perp. sissid (aka: sissid disphenoid)
---- 8D----
(Just some) Convex Segmentozetta (up)
---- 9D----
(Just some) Convex Segmentoyotta (up)
----- 10D-----
(Just some) Convex Segmentoxenna (up)
[8]ページ先頭





