Movatterモバイル変換

Segmentotopes

• Segmentotopes
• Convex Segmentochora (4D)
  • Cases with Tetrahedral Axis
  • Cases with Octahedral Axis
  • Cases with Icosahedral Axis
  • Cases with n-Prismatic or n-Antiprismatic Axis
  • Non-Lace-Prismatics
  • Complete Table
  • Close Relatives
  • Further Reading
• Convex Segmentotera (5D)
• Convex Segmentopeta (6D)
• Convex Segmentoexa (7D)
• Convex Segmentozetta (8D)
• Convex Segmentoyotta (9D)
• Convex Segmentoxenna (10D)
• Degenerate Segmentotopes

External links

In 2000 Klitzing published^[1] on segmentotopes in general resp. hisresearch on convex segmentochora in special. Segmentotopes are polytopes which bow to the following conditions:

• all vertices on the surface of 1 hypersphere
• all vertices on 2 parallel hyperplanes
• all edges of 1 length

The first condition shows that the circumradius is well defined. Moreover, in union withcondition 3 this implies that all 2D faces have to be regular. The sandwich type 2nd condition implies that all edges,which aren't contained completely within one of the hyperplanes, would join both, i.e. having onevertex each in either plane. Thence segmentotopes have to be monostratic. In fact,segmentotopes are the monostraticorbiforms. (Orbiforms, a terminus which had been created several years later only, just use the first and third condition of those.)Finally it follows, that the bases have to be orbiforms, while all the lacing elements have to be (lower dimensional) segmentotpes.

The naming of individual segmentotopes usually is based on the 2 base polytopes: top-base polytopeatopbottom-base polytope. Symbolically one uses the parallelness of those bases: P_top || P_bottom.(For the smaller segmentotopes the choice of bases need not be unique.)

Segmentotopes are closely related tolace prisms. In fact those concepts have a large common intersection,but they are not identical. While lace prisms need an axis of symmetry (in fact one which is describable as Dynkin symbol), one uses the terminus "axis" in the context of segmentotopes only in the sense of the line defined by the centers of the circumspheres of d-1 dimensional bases. (Thus the topic ofaxial polytopes does more relate to lace towers (asmultistratic generalizations of lace prisms) than to segmetotopes. None the less there is a large overlap.)– Note that the radius R of the d-1 dimensional circumsphere used for a segmentotpal base of dimension d-k might well be larger than the radiusr of its d-k dimensional circumsphere: for k > 1 the latter might well be placed within the former with some additional shifts:  R² = r² + s². For a simple example just considersquippy, the 4-fold pyramid,which is just half of anoct, when being considered asline ||triangle: the subdimensional base,the single edge, there is placed off-set.

In fact, letr_k be the individual circumradii of the bases, lets_k be the respective shifts away from the axis(if subdimensional), leth be the axial height andR the global circumradius, then we have the following interrelation formulabetween all these sizes  4 R² h² = ((r₂²+s₂²)-(r₁²+s₁²))² + 2 ((r₁²+s₁²)+(r₂²+s₂²)) h² + h⁴.

Convex Segmentochora   (up)

Just as polytopes are distinguished dimensionally as polygons, polyhedra, polychora, etc.so too are segmentotopes.
The onlysegmentogons (without any further adjectivic restriction) clearly are

• regular triangle   (point ||line) and
• square   (line ||line).

Segmentohedra already include infinite series like

• pyramids   (base being 2 < n/d < 6:  point ||{n/d}),
• prisms   (bases being 2 < n/d:  {n/d} ||{n/d}),
• antiprisms and retroprisms   (bases being 2 ≤ n/d resp. 3/2 < n/d < 2:  {n/d} ||{n/(n-d)}),
• cupolae andcuploids(*)   (top base being 6/5 < n/d < 6, d odd resp. even:  {n/d} ||{2n/d}),
• cupolaic blends(*)   (top base being 6/5 < n/d < 6, d odd:  ( {2n/d}[2{n/d}]{2n/d} ) ||{4n/2d}).

(*) Grünbaumian bottom base understood to be withdrawn.
For convex ones d clearly has to be 1 and several of the above series then become finite.

Polychora generally have the disadvantage not being visually accessible.Segmentochora are not so hard for that:Just consider the 2 base polyhedra displayed concentrically, perhaps slightly scaled, while the lacings thenget slightly deformed. Mathematically speaking, axial projections (view-point at infinity) and central projections (finite view-point),either one being taken on the axis for sure, from 4D onto 3D generally are well "viewable" for such monostratic figures. Especially when using real 3D graphics (like the here used VRMLs) instead of further projections onto 2D as in usual pictures: Note that all pictures at "segmentochoron display" within individual polychoron files will be linked to such VRML files.

Cases with Tetrahedral Axis:

Cases with Octahedral Axis:

Cases with Icosahedral Axis:

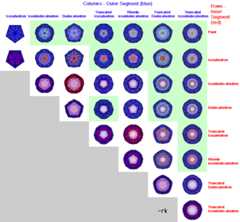
Cases with n-Prismatic or n-Antiprismatic Axis:

Non-Lace-Prismatics:

Just as already often was used within the set ofJohnson solids, several of the above segmentochora allowdiminishings too. Those generally break some symmetries of one or both bases, and therefore too of the axial symmetry.Thus there is no longer a unifying symmetry according to which aDynkin symbol could be designed,being the premise for lace prisms.Even though, such diminished ones are fully valid segmentotopes (following the above 3 conditions). An easy 3D example could be againline ||triangle,the alternate description of the above mentionedsquippy. The easiest 4D one clearly issquasc (i.e. the 1/4-lune of thehex).–Gyrations in some spare cases might apply as well,although those in general would conflict to the requirement of exactly 2 vertex layers.

But there is also a generic non-lace-prismatic convex segmentochoron with octahedral symmetry at one base,with icosahedral symmetry at the other. (The common subsymmetry clearly is the pyrital. But that one does not bow to Dynkin symbol description.)That one uses as faces 1cube (as bottom base), 6trip (asline ||square), 12squippy (astriangle ||line),8tet (astriangle ||point), and1ike (as top base).

Full Table:

K-4.1pen = pt || tet        (regular)K-4.1.1= line || perp {3}

K-4.2hex = tet || dual tet     (regular)K-4.3octpy = pt || oct         (segment ofhex)K-4.3.1= {3} || gyro tetK-4.4squasc = pt || squippy    (luna ofhex)K-4.4.1= line || tetK-4.4.2= {3} || incl {3}K-4.4.3= line || perp {4}

K-4.5rap = tet || oct            (uniform)K-4.6traf = tet || squippy       (segment ofrap)K-4.6.1= {3} || octK-4.6.2= {3} || gyro tripK-4.7trippy = line || squippy    (segment ofrap)K-4.7.1= {3} || tetK-4.7.2= pt || tripK-4.7.3= {3} || otho {4}   (where 1 {3}-edge || 2 {4}-edges)K-4.8bidrap = {3} || squippy     (wedge ofrap)K-4.8.1= {4} || tetK-4.8.2= line || ortho trip

K-4.9tepe = tet || tet        (uniform)K-4.9.1= line || para tripK-4.9.2= {4} || ortho {4}

K-4.10triddip = {3} || trip         (uniform)K-4.11ope = oct || oct              (uniform)K-4.11.1= trip || gyro tripK-4.12squippyp = squippy || squippy (segment ofope)K-4.12.1= {4} || tripK-4.12.2= line || cubeK-4.13digytpuf = trip || refl ortho trip (gyratedope)

K-4.14squaf = {4} || squap     (wedge ofoct || cube)K-4.14.1= {4} || gyro cubeK-4.15octacube = oct || cubeK-4.16squippy || gyro cubeK-4.17squappy = {4} || gyro squippyK-4.17.1= pt || squap

K-4.18tisdip = trip || trip (uniform)K-4.18.1= {4} || cube

K-4.19squappip = squap || squap    (uniform)K-4.19.1= cube || gyro cube

K-4.20tes = cube || cube       (regular)K-4.21cubaike = cube || ikeK-4.22paf = {5} || papK-4.22.1= {5} || gyro pipK-4.23tetaco = tet || co       (segment ofspid)K-4.24tet || tricu             (luna ofspid)K-4.25tricuf = {3} || tricu    (luna ofspid)K-4.25.1= {6} || tripK-4.26cubpy = {4} || squippy   (segment ofico)K-4.26.1= pt || cubeK-4.27traw = {3} || gyro tricu (luna ofico)K-4.27.1= {6} || octK-4.28bidoctaco = {4} || co    (wedge ofico)K-4.29octaco = oct || co       (segment ofico)K-4.30octatricu = oct || tricu (luna ofico)K-4.31squippiaco = squippy || coK-4.32squippiatricu = squippy || tricuK-4.33trateddi = {3} || teddi

K-4.34trapedip = {5} || pip (uniform)

K-4.35cubaco = cube || co

K-4.36ipe = ike || ike             (uniform)K-4.37gyepippip = gyepip || gyepipK-4.38peppyp = peppy || peppyK-4.38.1= line || pipK-4.39pappip = pap || papK-4.39.1= pip || gyro pipK-4.40mibdip = mibdi || mibdiK-4.41teddipe = teddi || teddi

K-4.42squipdip = pip || pip (uniform)

K-4.43cope = co || co          (uniform)K-4.44tobcupe = tobcu || tobcuK-4.45tricupe = tricu || tricuK-4.45.1= trip || hip

K-4.46haf = {6} || hapK-4.46.1= {6} || gyro hip

K-4.47thiddip = {6} || hip (uniform)

K-4.48coatut = co || tutK-4.49tobcuatut = tobcu || tutK-4.50tricuatut = tricu || tutK-4.51tripuf = {6} || tricuK-4.51.1= {3} || hipK-4.52octatut = oct || tut

K-4.53happip = hap || hap      (uniform)K-4.53.1= hip || gyro hip

K-4.54shiddip = hip || hip  (uniform)K-4.55tuta = tut || inv tut (segment ofrit)K-4.56tetatut = tet || tut  (segment ofrit)

K-4.57tuttip = tut || tut (uniform)

K-4.58oaf = {8} || oapK-4.58.1= {8} || gyro op

K-4.59todip = {8} || op (uniform)

K-4.60sniccup = snic || snic (uniform)

K-4.61coasirco = co || sircoK-4.62coaescu = co || escuK-4.63coaop = co || opK-4.64squaw = {4} || gyro squacuK-4.64.1= {8} || squap

K-4.65oappip = oap || oap    (uniform)K-4.65.1= op || gyro op (uniform)

K-4.66sircope = sirco || sirco  (uniform)K-4.67   esquigybcupe = esquigybcu || esquigybcuK-4.68escupe = escu || escuK-4.69squacupe = squacu || squacuK-4.69.1= cube || opK-4.70sodip = op || op          (uniform)K-4.71cubasirco = cube || sirco (segment ofsidpith)K-4.72   cube || esquibcuK-4.73squicuf = {4} || squacu   (wedge ofsidpith)K-4.73.1= {8} || cube

K-4.74dope = doe || doe (uniform)

K-4.75sircoatoe = sirco || toe

K-4.76tutatoe = tut || toe (segment ofprip)

K-4.77doaid = doe || idK-4.78ikadoe = ike || doe        (segment ofex)K-4.79   gyepip || doeK-4.80pappy = {5} || gyro peppyK-4.80.1= pt || papK-4.81papadoe = pap || doeK-4.82mibdiadoe = mibdi || doeK-4.83teddi adoe = teddi || doeK-4.84ikepy = pt || ike          (segment ofex)K-4.85   gyepippy = pt || gyepipK-4.86peppypy = pt || peppy      (wedge ofex)K-4.86.1= line || perp {5}K-4.87mibdipy = pt || mibdiK-4.88teddipy = pt || teddi

K-4.89tope = toe || toe (uniform)

K-4.90iddip = id || id (uniform)K-4.91   pobrope = pobro || pobroK-4.92perope = pero || pero

K-4.93   daf = {10} || dapK-4.93.1     = {10} || gyro dip

K-4.94tradedip = {10} || dip (uniform)

K-4.95coatoe = co || toe (segment ofrico)

K-4.96dappip = dap || dap      (uniform)K-4.96.1= dip || gyro dip

K-4.97squadedip = dip || dip (uniform)

K-4.98toatic = toe || tic

K-4.99ticcup = tic || tic      (uniform)K-4.100sircoatic = sirco || tic (segment ofsrit)K-4.101   esquigybcu || ticK-4.102   sircoagytic = sirco || gyro ticK-4.103   escu || ticK-4.104   escu || gyro ticK-4.105squipuf = {8} || squacu  (segment ofsrit)K-4.105.1= {4} || opK-4.106opatic = op || tic       (segment ofsrit)K-4.107octasirco = oct || sirco (segment ofspic)K-4.108   squippy || escuK-4.109squippy || squacu

K-4.110sniddip = snid || snid (uniform)

K-4.111sriddip = srid || srid    (uniform)K-4.112   gyriddip = gyrid || gyridK-4.113   pabgyriddip = pabgyrid || pabgyridK-4.114   mabgyriddip = mabgyrid || mabgyridK-4.115   tagyriddip = tagyrid || tagyridK-4.116   diriddip = dirid || diridK-4.117pecupe = pecu || pecuK-4.117.1= pip || dipK-4.118   pagydriddip = pagydrid || pagydridK-4.119   magydriddip = magydrid || magydridK-4.120   bagydriddip = bagydrid || bagydridK-4.121   pabidriddip = pabidrid || pabidridK-4.122   mabidriddip = mabidrid || mabidridK-4.123   gybadriddip = gybadrid || gybadridK-4.124   tedriddip = tedrid || tedrid

K-4.125gircope = girco || girco (uniform)

K-4.126sridati = srid || ti

K-4.127tipe = ti || ti (uniform)

K-4.128ticagirco = tic || girco (segment ofproh &srico)K-4.129coatic = co || tic       (segment ofsrico)

K-4.130tiddip = tid || tid (uniform)

K-4.131idasrid = id || srid (segment ofrox)K-4.132   id || dridK-4.133paw = {5} || gyro pecuK-4.133.1= {10} || papK-4.134   id || pabidridK-4.135   id || mabidridK-4.136   id || tedridK-4.137ikaid = ike || id    (segment ofrox)K-4.138   gyepip || idK-4.139peppia pero = peppy || peroK-4.140gyepipa pero = gyepip || peroK-4.141pippy = {5} || peppy (segment ofrox)K-4.141.1= pt || pipK-4.142papaid = pap || idK-4.143   mibdi || idK-4.144   pap || peroK-4.145   mibdi || peroK-4.146{5} || peroK-4.147teddi aid = teddi || idK-4.148   teddi || pero

K-4.149toagirco = toe || girco (segment ofprico)

K-4.150griddip = grid || grid (uniform)K-4.151tiatid = ti || tid

K-4.152doasrid = doe || srid (segment ofsidpixhi)K-4.153   doe || dridK-4.154pecuf = {5} || pecu   (wedge ofsidpixhi)K-4.154.1= {10} || pipK-4.155doa pabidrid = doe || pabidridK-4.156   doe || mabidridK-4.157   doe || tedrid

K-4.158idati = id || ti (segment ofsrix)

K-4.159sridatid = srid || tid (segment ofsrahi)K-4.160   gyrid || tidK-4.161   pabgyrid || tidK-4.162   mabgyrid || tidK-4.163   tagyrid || tidK-4.164   drid || tidK-4.165pepuf = {10} || pecu   (segment ofsrahi)K-4.165.1= {5} || dipK-4.166   pagydrid || tidK-4.167   magydrid || tidK-4.168   bagydrid || tidK-4.169   pabidrid || tidK-4.170   mabidrid || tidK-4.171   gybadrid || tidK-4.172   tedrid || tid

K-4.173tidagrid = tid || grid (segment ofprix)

K-4.174n-af = {n} || n-apK-4.174.1= {n} || gyro n-p

K-4.1753,n-dip = {n} || n-p (uniform)

K-4.176n-appip = n-ap || n-ap    (uniform)K-4.176.1= n-p || gyro n-p

K-4.1774,n-dip = n-p || n-p (uniform)

(For degenerate segmentochora, i.e. having zero heights, cf. page "finite flat complexes".)

Close Relatives:

1. In 2012 two sets of closely related monostratic polytopes where found:

   • n-py || inv gyro n-py   (2<n<6)   and
   • n-cu || inv gyro n-cu   (6/5<n<6).

   In fact the constraint, of the lacing edges all having unit lengths too, results in some specific shift values for the base polyhedra.As those base polyhedra on the other hand are not degenerate, this conflicts to having a common circumsphere in general: within thecase of pyramids only the special value n=3 results in a true convex segmentochoron (being thehex), within thecase of cupolae only the special value n=2 results in a true convex segmentochoron (beingtrip || refl ortho trip).Even though, the values n=3,4,5 resp. n=2,3,4,5 would well generate monostratic convex regular-faced polychora (CRFs).

   The closeness even could be pushed on a bit. If one of the (equivalent) bases each, which are segmentohedra in turn, would be diminished by omitting the smaller top face, i.e. maintaining therefrom only the larger bottom face, those would re-enter the range of valid segmentochora again:{n} || gyro n-py resp.{2n} || n-cu. In fact, here the necessary shifts of the bases could be assembled at the degenerate base alone. There a non-zero shift is known to be allowed.

   Without narrowing those findings, those 2 families could be de-mystified a bit by using different axes: the pyramidal case is nothing but the bipyramid of the n-antiprism, while the cupolaic case is nothing but the bistratic lace towerxxo-n-oxx oxo&#xt.

   Later the author realised also the existance of their ortho counterparts:

   • n-py || inv ortho n-py   (2<n<6)   and
   • n-cu || inv ortho n-cu   (6/5<n<6).

   Again those can be splitted at their now always prismatic pseudofacial equatorFor the pyramidal ones, the case n=2 becomes subdimensional, there representing nothing but theoct.The general case here is nothing but the n-prismatic bipyramid.For the cupolaic case N=2 clearly is full dimensional, but pairs of containedsquippies becomecorealmic and thus unite intoocts. Therefore that case happens to become nothing butope.

2. In 2014 three close relatives to pyramids have been found, which are not orbiform just because their base is not. Those areline || bilbiro,{3} || thawro, resp.{5} || pocuro. A further such case would beline || esquidpy.

3. Besides of considering 2 parallel hyperplanes cutting out monostratic layers of larger polychora, in 2012 (and more deeply in 2013) considerations about 2 intersecting equatorial hyperplanes were done. Those clearly cut out wedges. The specific choice of those hyperplanesmade up the terminuslunae. Only theCRF ones were considered. The followinglunae are known so far:

   • Lunae ofhex: cells beingsquippy andtet
     • 1/4-luna ofhex =squasc = pt ||squippy(thus a segmentochoron) – hyperplanes intersect at 90°.
   • Lunae ofico: cells beingtricu,oct, andsquippy
     • 2/6-luna ofico =oct || tricu(thus a segmentochoron) – hyperplanes intersect at 120°.
     • 1/6-luna ofico ={3} || gyro tricu(thus a segmentochoron) – hyperplanes intersect at 60°.
   • Lunae ofex: cells beingpero,peppy, andtet
     • 4/10-luna ofex – hyperplanes intersect at 144°.
     • 3/10-luna ofex – hyperplanes intersect at 108°.
     • 2/10-luna ofex – hyperplanes intersect at 72°.
     • 1/10-luna ofex – hyperplanes intersect at 36°.
   • Lunae ofspid resp.gyspid: cells beingtricu,tet, andtrip
     • 0.290215-luna ofspid =tet || tricu(thus a segmentochoron) – hyperplanes intersect at   arccos(-1/4) = 104.477512°.
     • 0.209785-luna ofspid ={3} || tricu(thus a segmentochoron) – hyperplanes intersect at   arccos(1/4) = 75.522488°.
     • 0.419569-luna ofgyspid ={3} || tricu || {3}– hyperplanes intersect at   2 arccos(1/4) = arccos(-7/8) = 151.044976°.
   • Lunae ofquawros: cells beingsquacu,cube,tet, andtrip
     • 1/4-luna ofquawros – hyperplanes intersect at 90°.
   • Lunae ofstawros: cells beingpecu,pip,tet, andtrip
     • 2/5-luna ofstawros – hyperplanes intersect at 144°.

4. Surely the convexity restriction could be released. Some3D examples can be found on the page onaxials.
   Some4D cases would be e.g.
   • 0.591923 -gissidpy = pt || gissid =oo3oo5/2ox&#x
   • 0.613502 -quithpy = pt || quith =oo3ox4/3ox&#x
   • 0.618034 -gikepy = pt || gike =ox3oo5/2oo&#x
   • 0.618034 -sissidpy = pt || sissid =ox5/2oo5oo&#x
   • 0.618034 -stasc = line || perp {5/2} =xo ox5/2oo&#x
   • 0.618034 -gissidragike = narrower gissid || gike =ox3oo5/3xo&#x
   • 0.618034 -shallower gissidasissid = gissid || sissid (with lacing starps)
   • 0.621876 -ogasc = line || perp {8/3} =xo ox4/3ox&#x
   • 0.658240 -shasc = line || perp {7/2} =xo ox7/2oo&#x
   • 0.662791 -gissidagike = taller gissid || gike =ox3oo5/2xo&#x
   • 0.662791 -taller gissidasissid = gissid || sissid (with lacing staps)
   • 0.662791 -stapepy = point || stap =oxo5/2oox&#x
   • 0.692924 -gissidagid = gissid || gid =oo3ox5/2xo&#x
   • 0.726543 -gikagid = gike || gid =xo3ox5/2oo&#x
   • 0.707107 -hossdap = pseudo sissid || pseudo sissid =reduced( β2β5o5/2o , by β5o5/2o )
   • 0.707107 -starpglassit = stappy || inv stappy =xooo5/2ooxo&#xr
   • 0.707107 -tho = tet || dual pseudo tet =hemi( x3o3/2o3o3*a )
   • 0.707107 -fitetaltet = faceted tet || dual tet =reduced( xx3/2ox3oo&#x , by x3/2x )
   • 0.739539 -quith || "thah-squares star" =reduced( xo4/3xx3/2ox&#x , by oct )
   • 0.774597 -tutrippapy = pt || tutrip =reduced( oox4/2oxx&#x , by ..x4/2..x )
   • 0.774597 -tubidrap = pseudo {4} || so =reduced( oxx4/2xox&#x , by ..x4/2..x )
   • 0.774597 -firp = tet || pseudo 2thah =reduced( xx3/2oo3ox&#x , by x3/2o3x )
   • 0.774597 -fitetaoct = faceted 3tet || oct =reduced( ox3/2xx3oo&#x , by x3/2x )
   • 0.774597 -hotetahoct = pseudo tet || pseudo oct =reduced( xx3/2ox3oo3*a&#x , by x3/2x )
   • 0.774597 -pafirp = tet || "thah-squares star" =reduced( xx3/2xo3ox&#x , by x3/2x )
   • 0.774597 -{3} || pseudo gyro trip =reduced( ox xx3/2ox&#x , by x3/2x )
   • 0.780850 -tistadip = {5/2} || stip =x3o x5/2o
   • 0.790569 -tutepe = pseudo {4} || {4/2}-prism =reduced( ox xo4/2xx&#x , by x.4/2x. )
   • 0.791345 -tistodip = {8/3} || stop =x3o x8/3o
   • 0.825168 -stappip = stap || stap =x s2s5/2s = narrower stip || stip =xx xo5/2ox&#x
   • 0.866025 -"coord-axes edge star" || cube
   • 0.874032 -stacupe = stip || 2pip =xx5/2ox&#x
   • 0.874032 -quit sissidagird = quit sissid || gird =reduced( ox5/4xx5/3xx&#x , by x5/4x )
   • 0.879465 -"thah-squares star" || cube
   • 0.881132 -sistadip = stip || stip =x4o x5/2o
   • 0.890446 -cubaquerco = cube || querco =ox3/2oo4xx&#x
   • 0.890446 -sistodip = stop || stop =x4o x8/3o
   • 0.912871 -"coord-planes square star" || cube
   • 0.951057 -sidtidap = sidtid || gyro sidtid =xo5/2ox3oo3*a&#x
   • 0.951057 -gidtidap = gidtid || gyro gidtid =xo5/4ox3oo3*a&#x
   • 0.951057 -ditdidap = ditdid || gyro ditdid (the blend of the latter 2)
   • 1              -sidtidpy = pt || sidtid =xo3oo3oo5/2*b&#x
   • 1              -gidtidpy = pt || gidtid =xo3oo3/2oo5*b&#x
   • 1              -ditdidpy = pt || ditdid =xo5oo3/2oo5/2*b&#x
   • 1              -tetacho = tet || cho =reduced( ox3/2ox3xx&#x , by x3/2x )
   • 1              -hotet aoho = pseudo 2tet || oho =reduced( xx3/2oo3ox3*a&#x , by x.3/2o.3o.3*a )
   • 1              -sissidagad = sissid || gad =xo5/2oo5ox&#x
   • 1              -co retro-cuploid = "thah-squares star" || co =reduced( ox3/2xx4oo&#x, by .x3/2.x4.o )
   • 1              -hoctaoho = pseudo 2oct || oho =reduced( xx3/2xo3ox3*a&#x, by x.3/2x.3o.3*a )
   • 1              -octacho = oct || cho =reduced( ox3/2xx3ox&#x, by x3/2x )
   • 1              -hothahacho = pseudo thah || cho =reduced( xx3/2ox3xx&&#x, by x3/2x )
   • 1              -gikaike = gike || ike
   • 1              -sirgikaike (edge-faceting ofgikaike)
   • 1              -girgikaike (edge-faceting ofgikaike)
   • 1              -cubagike = cube || gike
   • 1.064815 -gaddadid = gad || did =xo5ox5/2oo&#x
   • 1.064815 -sissidadid = sissid || did =oo5ox5/2xo&#x
   • 1.082392 -quithaquitco = quith || quitco =ox3xx4/3xx&#x
   • 1.120533 -tiggia gaquatid = tiggy || gaquatid =xx3xx5/3ox&#x
   • 1.136572 -gidtidagiid = gidtid || giid =oo3/2ox3xx5*a&#x
   • 1.183216 -ohoa hotut = oho || pseudo 2tut =reduced( xx3/2xo3xx3*a&#x, by x.3/2x.3o.3*a )
   • 1.183216 -choatut = cho || tut =reduced( ox3/2xx3xx&#x, by x3/2x )
   • 1.328131 -gaddaraded = gad || raded =xx5oo5/2ox&#x
   • 1.336349 -dida raded = raded || tigid =xx5ox5/2xo&#x
   • 1.414214 -didadoe = did || doe =reduced( oo5xx5/2ox&#x, by x5/2x )
   • 1.414214 -goccoa cotco = gocco || cotco =xx3ox4xx4/3*a&#x
   • 1.432173 -radedadoe = raded || doe =reduced( ox5xo5/2xx&#x , by x5/2x )
   • 1.618034 -gadadoe = gad || doe
   • 1.765796 -siida = siid || gyro siid =xo5/2ox3xx3*a&#x
   • 2.363565 -radeda tigid = did || tigid =ox5xx5/2oo&#x
   • 2.497212 -sissidaraded = sissid || raded =ox5oo5/2xx&#x
   • 3.835128 -sidtidasiid = sidtid || siid =xx5/2oo3ox3*a&#x
   • 4.352502 -diddatigid = did || tigid =ox5xx5/2oo&#x
   • 4.684471 -gidditdid aidtid = gidditdid || idtid =xx5/3xx3ox5*a&#x
   • ...             -n/d scalene = line || perp {n/d} =xo ox-n/d-oo&#x
   • ...
5. By means of externalblends at the bases multistratic stacks can be derived, right in the sense oflace towers. But in general,orbiformitythereby is lost. Only few are known, which then still are. Among those clearly are the ones which can be deduced asmultistratic segments of uniform or evenscaliform polytopes. But there arealso rare exceptional finds beyond those, e.g.
   • sidrebcu = sissid || (pseudo) did || gad =xoo5/2oxo5oox&#xt
   • ...

Further Reading

• ↑ Convex Segmentochora –(PDF)
  published as: "Convex Segmentochora", by Dr. R. Klitzing,Symmetry: Culture and Science, vol. 11, 139-181, 2000
• externallink (hosted by J. McNeill)

---- 5D----

(Just some) Convex Segmentotera   (up)

hix = pt || pen        (regular)= line || perp tet= {3} || perp {3}

tac = pen || dual pen     (regular)hexpy = pt || hex         (segment oftac)octasc = line || perp oct (lune oftac)squete = {3} || perp {4}  (wedge oftac)

hin = hex || gyro hex         (uniform)rappy = pt || rap             (segment ofhin)trafpy = pt || traf           (wedge ofhin                               segment ofrappy)bidrappy = pt || bidrap       (segment ofhin)trippasc = line || perp trip  (segment ofhin)editetaf = line || tepe       (segment ofhin)tetaf = tet || inv tepe       (segment ofhin)= tet || hexditetaf = {3} || gyro tepe    (wedge ofhin)= pen || gyro tripsquasquasc = {4} || squasc    (wedge ofhin)tedhin = {4} || hex           (wedge ofhin)bidhin = oct || hex           (wedge ofhin)= tet || inv rapdihin = pen || inv rap        (segment ofhin)nibdihin = pen || inv traf    (wedge ofhin)triddaf = trip || bidual trip (wedge ofhin)

penp = pen || pen        (uniform)= line || tepe= {4} || ortho trip

rix = pen || rap                    (uniform)tepepy = pt || tepe                 (segment ofrix)octatepe = oct || tepe              (segment ofrix)bidrix = pen || bidrap              (segment ofrix)= squippy || ortho tepetedrix = {4} || lacing-ortho ( {4} || lacing-ortho {4} )= {4} || ortho tepe          (wedge ofrix)trial triddip = {3} || gyro triddip (segment ofrix)

tratet = tet || tepe               (uniform)= {3} || triddip= trip || lacing-ortho trip

hexip = hex || hex                      (uniform)= tepe || inv. tepeoctpyp = line || ope                    (segment ofhexip)= octpy || octpysquascop = {4} || part. ortho cube      (segment ofhexip)= squasc || squascdot = rap || inv rap                    (uniform)triddippy = pt || triddip               (segment ofdot)tetcubedaw = {2}-ap || axis-ortho {4}-p (lune ofdot)teta ope = tet || ope                   (segment ofdot)= oct || raptaope = {3} || ope                      (wedge ofdot)tridafup = triddip || bidual triddip    (segment ofdot)teddot = bidrap || gyro-inv bidrap      (diminishing ofdot)

squiddaf = {4}-prism || bidual {4}-prism (scaliform)cubaope = cube || ope

troct = oct || ope              (uniform)= triddip || gyro triddiptisquippy = {3} || tisdip       (segment oftroct)          = trip || triddip

rappip = rap || rap          (uniform)= ope || tepetraffip = trip || inv tisdip (segment ofrappip)tepacube = tepe || cube      (wedge ofrappip)

squatet = tepe || tepe              (uniform)= {4} || tisdip= cube || lacing-ortho cube

tratrip = trip || tisdip     (uniform)= triddip || triddip

squoct = ope || ope                         (uniform)= tisdip || {3}-gyro tisdipsquasquippy = {4} || tes                    (segment ofsquoct)cubasquasc = cube || squasc                 (segment oftraltisdip)traltisdip = {3} || gyro tisdiptisdipah = tisdip || {6}hexaico = hex || ico                        (segment ofrat)rapaspid = rap || spid                      (segment ofrat)opepy = pt || ope                           (segment ofrat)squippyippy = pt || squippyp                (segment ofrat)= line || cubpyhexaco = hex || co                          (lune ofrat)rapaco = rap || co                          (lune ofrat)octpy || octaco                             (lune ofrat)opeaco = ope || co                          (segment ofrat)opeah = ope || {6}                          (wedge ofrat)tripgytricudaw = trip || ortho-gyro tricu   (wedge ofrat)oct-first lune of rat = rap || tetaco       (lune ofrat)tet-first lune of rat = hex || octaco       (lune ofrat)= rap || alt. tetacopenatrip = pen || trip                      (wedge ofscad)penaspid = pen || spid                      (segment ofscad)tepaco = tepe || co                         (lune ofscad)pexhix = trip || axis-ortho base-para tricu (wedge ofscad)

piddaf = pip || bidual pip

tracube = cube || tes      (uniform)= tisdip || tisdip

petet = {5} || trapedip         (uniform)= pip || lacing-ortho pip

icoap = ico || dual ico (scaliform)coates = co || tesicates = tes || icotessap = hex || tes{4} || gyro tes         (wedge oftessap)

poct = trapedip || {3}-gyro trapedip (uniform)

trike = ike || ipe (uniform)

pent = tes || tes        (regular)icope = ico || ico       (uniform)opeacope = ope || cope   (segment oficope)cubpyp = line || tes     (segment oficope)trawp = ope || hip       (wedge oficope)= traw || trawspiddip = spid || spid   (uniform)tepeacope = tepe || cope (segment ofspiddip)tricufip = hip || tisdip= tricuf || tricuf

cubacope = cube || cope

trapip = pip || squipdip      (uniform)= trapedip || trapedip

traco = co || cope            (uniform)tritricu = triddip || thiddip (segment oftraco)

hatet = {6} || thiddip          (uniform)= hip || lacing-ortho hippexhix = {6} || triddip

squike = ipe || ipe (uniform)

opeatut = ope || tut            (wedge ofspix)copatut = cope || tut           (wedge ofspix)rapatut = rap || tut            (wedge ofspix)rapalsrip = rap || inv srip     (segment ofspix)spidasrip = spid || srip        (segment ofspix)tetacope = tet || cope          (segment ofspix)triddipa hip = {3} || tricupe   (wedge ofspix)= trip || tripuf= triddip || hiptripa thiddip = {6} || tricupe  (wedge ofspix)= trip || thiddippabex hix = thiddip || antipara thiddip (scaliform)triddip althiddip = triddip || gyro thiddip

pecube = squipdip || squipdip (uniform)

octhipdaw = {3}-ap || axis-ortho {6}-phoct = thiddip || {3}-gyro thiddip (uniform)hisquippy = {6} || shiddip         (segment ofhoct)squaco = cope || cope              (uniform)squatricu = tisdip || shiddip      (segment ofsquaco)          = tricupe || tricupeicarit = ico || rit            (segment ofnit)octco tuttric = octaco || tut  (wedge ofnit)= oct || coatut= co || octatutrapasrip = rap || srip         (segment ofnit)pabdinit = srip || inv srip    (scaliform,                                segment ofnit)octacope = oct || cope         (segment ofnit)trial tricupe = {3} || tricupe (wedge ofnit)tisdippy = pt || tisdip        (segment ofnit)ica tutcup = ico || tuta       (segment ofnit)coa tutcup = co || tuta        (wedge ofnit)coarit = co || rit             (wedge ofnit)

tessarit = tes || rit

trahip = thiddip || thiddip (uniform)= hip || shiddip

tepatut = tepe || tut         (wedge ofsiphin)tutaf = tut || inv tuttip     (wedge ofsiphin)tutas = tuta || alt. tuta     (scaliform,                               segment ofsiphin)rita = rit || gyro rit        (scaliform,                               segment ofsiphin)hexalrit = hex || gyro rit    (segment ofsiphin)octa tutcup = oct || tutatripalhip = trip || lacing-ortho hiptetco tuttric = tet || coatut (segment ofpenasrip)= co || tetatut= tut || tetacopenasrip = pen || sripspidatip = spid || tipsripaltip = srip || inv tip

srippip = srip || srip        (uniform)opeatuttip = ope || tuttip    (segment ofsrippip)copea tuttip = cope || tuttip (segment ofsrippip)tripufip = trip || shiddip    (wedge ofsrippip)         = tripuf || tripuf

rapatip = rap || tip        (segment ofsarx)sripatip = srip || tip      (segment ofsarx)coatuttip = co || tuttip    (segment ofsarx)trathiddip = {3} || thiddip (segment ofsarx)

pepip = pedip || pedip (uniform)

tratut = tut || tuttip (uniform)

hacube = shiddip || shiddip      (uniform)rittip = rit || rit              (uniform)tutcupip = tuttip || inv tuttip  (segment ofrittip)= tuta || tutatepeatuttip = tepe || tuttip     (segment ofrittip)= tetatut || tetatut

tippip = tip || tip (uniform)

squatut = tuttip || tuttip (uniform)

pennatip = pen || tip       (segment ofrin)tipadeca = tip || deca      (segment ofrin)octatuttip = oct || tuttip  (segment ofsibrid)sripadeca = srip || deca    (half ofsibrid)hatricu = thiddip || hiddip (half ofhaco)

otet = {8} || todip          (uniform)= op || lacing-ortho op

trasnic = snic || sniccup (uniform)

owoct = todip || {3}-gyro todip (uniform)

decap = deca || deca (uniform)

rita sidpith = rit || sidpithsirco acope = sirco || cope

trasirco = sirco || sircope (uniform)

tradoe = doe || dope (uniform)

squasnic = sniccup || sniccup (uniform)

ocube = sodip || sodip         (uniform)squasirco = sircope || sircope (uniform)sidpithip = sidpith || sidpith (uniform,                                segment ofscant)squicuffip = squicuf || squicuf (wedge ofsidpithip)= tes || op

squadoe = dope || dope (uniform)

toa sircope = toe || sircope

idadope = id || dope

ritag thex = rit || gyro thex (segment ofsirhin)thexa = thex || gyro thex     (scaliform,                               segment ofsirhin)teta tuttip = tet || tuttip   (segment ofsirhin)rapadeca = rap || deca        (segment ofsirhin)deca aprip = deca || prip     (segment ofsirhin)tutcupa toe = tuta || toe     (wedge ofsirhin)

tipalprip = tip || inv prip (segment ofcappix)tuttipa toe = tuttip || toe (wedge ofcappix)

triddippa hiddip = trddip || hiddip (segment ofcard)pripa = prip || inv prip            (segment ofcard)sripaprip = srip || prip            (segment ofcard)thexip = thex || thex               (uniform)

tratoe = toe || tope (uniform)

prippip = prip || prip            (uniform)tuttipa tope = tuttip || tope     (segment ofprippip)             = tutatoe || tutatoe

exip = ex || ex      (uniform)gappip = gap || gap  (uniform)sadip = sadi || sadi (uniform)

cuba sircope = cube || sircope

trid = id || iddip (uniform)

haop = hodip || hodip (uniform)

squatoe = tope || tope        (uniform)icathex = ico || thex         (segment ofsart)thexarico = thex || rico      (segment ofsart)sripalprip = srip || inv prip (segment ofsart)trashiddip = {3} || shiddip   (segment ofsart)cotut totric = co || tutatoe  (wedge ofsart)= coatut || toe= tut || coatoe

ricoasadi = rico || sadidoa iddip = doe || iddip

squid = iddip || iddip (uniform)

ricoa = rico || gyro rico (scaliform)

ricope = rico || rico       (uniform)copatope = cope || tope     (segment ofricope)         = coatoe || coatoe

coasircope = co || sircopeica sidpith = ico || sidpithricasrit = rico || sritricoaspic = rico || spic

pripalgrip = prip || gyro grip (segment ofpattix)tutatope = tut || tope         (segment ofpattix)

tratic = tic || ticcup (uniform)

ritarico = rit || rico   (segment ofspat)spidaprip = spid || prip (segment ofspat)pripagrip = prip || grip (segment ofspat)gripa = grip || inv grip (segment ofspat)copatoe = cope || toe    (wedge ofspat)

grippip = grip || grip (uniform)

ticca sircope = tic || sircopesquatic = ticcup || ticcup (uniform)spiccup = spic || spic     (uniform)srittip = srit || srit     (uniform,                            segment ofspan)sidpith || srit            (segment ofspan)

deca agrip = deca || grip (segment ofpirx)

cuba octu = cube || octu

twacube = sitwadip || sitwadip (uniform)

taha = tah || gyro tah (scaliform,                        segment ofpirhin)tipagrip = tip || grip

tahp = tah || tah (uniform)

tattip = tat || tat (uniform)srit || tat         (segment ofsirn)rap || tip          (segment ofsirn)sircoa ticcup = sirco || ticcup (segment ofsirn){4} || todip        (segment ofsirn)

trasnid = snid || sniddip (uniform)

ricatah = rico || tah    (segment ofsibrant)sripagrip = srip || grip (segment ofsibrant)coatope = co || tope     (wedge ofsibrant)

squasnid = sniddip || sniddip (uniform)

gippiddip = gippid || gippid (uniform)

trasrid = srid || sriddip (uniform)

gripagippid = grip || gippid (segment ofcograx)

squasrid = sriddip || sriddip (uniform)

thexagtah = thex || gyro tah

tragirco = girco || gircope (uniform)

squagirco = gircope || gircope (uniform)prittip = prit || prit         (uniform)

trati = ti || tipe (uniform)

squati = tipe || tipe (uniform)

ritasrit = rita || sritsricoa = srico || gyro srico     (scaliform)prohalsrico = proh || gyro srico (diminishing ofsricoa)

tico || prissi

prohp = proh || proh     (uniform,                          segment ofcarnit)prit || proh             (segment ofcarnit)prit || srit             (segment ofcarnit)hodip || tisdip          (segment ofcarnit)sricope = srico || srico (uniform)

ticope = tico || tico (uniform)

pripa gippid = prip || gippid (segment ofpattit)

proh || tat (segment ofcapt)

tahatico = tah || tico (segment ofpirt)

tratid = tid || tiddip (uniform)

grittip = grit || grit (segment ofprin)

squatid = tiddip || tiddip (uniform)

roxip = rox || rox (uniform)

prohagrit = proh || grit  (segment ofpattin)ticca gircope = tic || gircope

contip = cont || cont (uniform)

pricoa = prico || gyro prico (scaliform)

pricope = prico || prico       (uniform)gidpithip = gidpith || gidpith (uniform,                                segment ofcogart)

hipe = hi || hi (uniform)

tragrid = grid || griddip (uniform)

squagrid = griddip || griddip (uniform)

gritta gidpith = grit || gidpith (segment ofcogrin)

gricoa = grico || gyro grico (scaliform)

gricope = grico || grico (uniform)

rahipe = rahi || rahi (uniform)

thipe = thi || thi (uniform)

texip = tex || tex (uniform)

grixip = grix || grix (uniform)

gippiccup = gippic || gippic (uniform)

sidpixhip = sidpixhi || sidpixhi (uniform)

srixip = srix || srix (uniform)

srahip = srahi || srahi (uniform)

xhip = xhi || xhi (uniform)

prahip = prahi || prahi (uniform)

prixip = prix || prix (uniform)

grahip = grahi || grahi (uniform)

gidpixhip = gidpixhi || gidpixhi (uniform)

3,n-dippip = n-p || 4,n-dip     (uniform)= 3,n-dip || 3,n-dip

n,cube-dip = 4,n-dip || 4,n-dip (uniform)

n,m-dippip = n,m-dip || n,m-dip (uniform)

(n,m-ap)-dip = n,m-dip || para-gyro n,m-dip (uniform)

n,m-dafup = n,m-dip || bidual n,m-dip (scaliform)

n-daf = n-p || bidual n-p (scaliform)

(n, dual n, n-p)-tric = n-g || gyro 3,n-dip

(n, n-p, gyro n-p)-tric = n-g || n-appip

(For degenerate segmentotera, i.e. having zero heights, cf. page "finite flat complexes".)

Somenon-convex segmentotera would be:

• 0.623054 -stadow = pentagram || fully perp. pentagram (aka: star disphenoid)
• 0.629640 -ogdow = octagram || fully perp. octagram (aka: octagram disphenoid)
• 0.633157 -quithesc = line || fully perp. quith (aka: quith scalene)
• 0.636010 -sissidisc = line || fully perp. sissid (aka: sissid scalene)
• 0.636010 -state = triangle || fully perp. pentagram (aka: star tettene)
• 0.636010 -gogishiragax = narrower gogishi || gax (aka: gogishi-gax retroprism)
• 0.638475 -togdow = triangle || fully perp. octagram (aka: triangle-octagram disphenoid)
• 0.667731 -gogishiagax = taller gogishi || gax (aka: gogishi-gax antiprism)
• 0.674163 -shadow = small heptagram || fully perp. small heptagram (aka: small heptagrammic disphenoid)
• 0.680827 -gashia = gashi || dual gashi (aka: gashi antiprism)
• 0.707107 -bostarpglassdit =oxo(-x) xooo5/2ooxo&#xr
• 0.707107 -hehad = pen || dual pseudo pen (aka: demicross)
• 0.707107 -phap = (non-convex) pen || dual pen (aka: pennic hemiantiprism)
• 0.707107 -nophap = pseudo pen || dual pseudo pen (aka: spinopennic hemiantiprism)
• 0.707107 -sistadow = square || fully perp. pentagram (aka: (square,star)-disphenoid)
• 0.816497 -firx = pen || firp
• 0.951057 -gadtaxhiap = gadtaxhi || alt. gadtaxhi (aka: gadtaxhi alterprism, uniform)
• 0.951057 -gadtaxadiap = gadtaxady || alt. gadtaxady (aka: gadtaxady alterprism)
• 1.050501 -gicalico = gico || dual ico (aka: blend of 3 icateses)
• 1.074481 -sishia = narrower sishi || sishi (aka: sishi alterprism)
• 1.125151 -pirgadia = pirgady || alt. pirgady (aka: pirgady alterprism)
• 1.209137 -traquitco = quitco || quitcope
• 1.248606 -ragashia = ragashi || inv ragashi (aka: ragashi alterprism)
• 1.618034 -sirgashia = sirgashi || inv sirgashi (aka: sirgashi alterprism)
• 1.666693 -sirgaship = sirgashi || sirgashi (aka: sirgashi prism)
• 1.677756 -sutia = suti || alt. suti (aka: suti alterprism)
• 1.693527 -gohip = gohi || gohi (aka: gohi prism, uniform)
• 1.917564 -righia = righi || inv righi (aka: righi alterprism)
• 2.321762 -sidtaxhiap = sidtaxhi || alt. sidtaxhi (aka: sidtaxhi alterprism, uniform)
• 2.321762 -sirdtaxadiap = sirdtaxady || alt. sirdtaxady (aka: sirdtaxady alterprism)
• 2.352869 -ditdia = ditdi || alt. ditdi (aka: ditdi alterprism)
• 2.527959 -sid pippadia = narrower sid pippady || sid pippady (aka: sid pippady alterprism)
• 2.829949 -rasishia = narrower rasishi || rasishi (aka: rasishi alterprism)
• 3.118034 -sophip = sophi || sophi (aka: sophi prism)
• 3.404434 -sirghia = sirghi || inv sirghi (aka: sirghi alterprism)
• 3.423760 -sirghipe = sirghi || sirghi (aka: sirghi prism)
• 3.855219 -stut phiddixa = stut phiddix || alt. stut phiddix (aka: stut phiddix alterprism)
• 4.923348 -pirghia = pirghi || inv pirghi (aka: pirghi alterprism)
• 5.345177 -wavhiddixa = wavhiddix || alt. wavhiddix (aka: wavhiddix alterprism)
• 6.893126 -sphiddixa = sphiddix || alt. sphiddix (aka: sphiddix alterprism)

---- 6D----

(Just some) Convex Segmentopeta   (up)

hop = pt || hix        (regular)= line || perp pen= {3} || perp tet

gee = hix || inv hix      (regular)tacpy = pt || tac         (segment ofgee)hexasc = line || perp hex (lune ofgee)octete = {3} || perp oct  (wedge ofgee)squepe = {4} || perp tet  (wedge ofgee)

hixip = hix || hix                (uniform)= line || penp= trip || part. ortho tripdijak = hin || tac                (segment ofjak)tedjak = hex || hin               (scaliform,                                    tridiminishedjak)hedjak = {4} || hin               (wedge ofjak)hinpy = pt || hin                 (segment ofjak)dihinpy = pt || dihin             (segment ofjak)rapesc = line || perp rap         (segment ofjak)tripal triddip = trip || dual-perp triddip                                  (wedge ofjak)hixalrix = hix || inv rix         (segment ofjak)hixaltriddip = hix || alt triddip (wedge ofjak)penaf = pen || inv penp           (segment ofjak)rapalpenp = rap || inv penp       (segment ofjak)trippete = {3} || perp trip       (segment ofjak)

ril = hix || rix                  (uniform)penppy = pt || penp               (segment ofril)rapa penp = rap || penp           (segment ofril)trial tratet = {3} || dual tratet (segment ofril)octa tratet = oct || tratet       (segment ofril)tidril = hix || tedrix            (wedge ofril)pedril = {4} || tratet            (segment ofril)

trapen = pen || penp   (uniform)= {3} || tratet

hax = hin || gyro hin          (uniform)taccup = tac || tac            (uniform)tetdip = tet || tratet         (uniform)tratetdafup = tratet || bidual tratet (scaliform)tetal tratet = tet || inv tratettepasc = line || perp teperixpy = pt || rix              (segment ofhax)hixadot = hix || dot           (segment ofhax)hixacube = hix || cube         (wedge ofhax)rixa = rix || inv rix          (scaliform,                                segment ofhax)hexaf = hex || gyro hexip      (segment ofhax)octatepepy = pt || octatepe    (wedge ofhax)= tet || rappy= oct || tepepyhixa tetaope = hix || teta ope (half ofhax)hixaope = hix || ope           (quarter ofhax)tritra ope = (trig, dual trig, para trip, gyro trip) lace simplex

trahex = hex || hexip (uniform)

trial troct = {3} || gyro troct

bril = rix || dot                        (uniform)tratetpy = pt || tratet                  (segment ofbril)tratet altroct = tratet || gyro troct    (segment ofbril)teta troct = tet || troct                (segment ofbril)pena rappip = pen || rappip              (segment ofbril)rappaf = rap || inv. rappip              (segment ofbril)triddippa tridafup = triddip || tridafup (segment ofbril)tisdip altratet = tisdip || gyro tratettatraffip = {3} || traffip= trip || gyro tisquippy= traf || tisdip

hinnip = hin || hin                (uniform)= hexip || alt hexiptetafip = tepe || inv squatet      (segment ofhinnip)        = tepe || hexippenpal rappip = penp || alt rappip (segment ofhinnip)              = dihin || dihinrappyp = line || rappip            (segment ofhinnip)

squapen = penp || penp   (uniform)= {4} || squatet

rixip = rix || rix         (uniform)tepepyp = line || squatet  (segment ofrixip)        = tepepy || tepepy

trarap = rap || rappip                 (uniform)= tratet || trocttitraf = triddip || gyro-para tratrip  (segment oftrarap)

dotip = dot || dot                (uniform)= rappip || inv rappiptridafupip = tridafup || tridafup (segment ofdotip)= tratrip || bidual tratripsquahex = hexip || hexip          (uniform)hixascad = hix || scad            (segment ofstaf)spidapenp = spid || penp          (segment ofstaf)hexippy = pt || hexip             (segment ofrag)hexipaico = hexip || ico          (wedge ofrag)hexipaco = hexip || co            (wedge ofrag)taccarat = tac || rat             (segment ofrag)hexarat = hex || rat              (segment ofrag)rixascad = rix || scad            (segment ofrag)dotpy = pt || dot                 (segment ofmo)dottascad = dot || scad           (segment ofmo)hinro = hin || rat                (segment ofmo)hinatedrat = hin || tedrat        (segment ofmo)icoahin = ico || hin              (segment ofmo)hinaco = hin || co                (segment ofmo)penal rappip = pen || alt rappip  (segment ofmo)spidarappip = spid || rappip      (wedge ofmo)tetaopepy = pen || ope            (wedge ofmo)= tet || opepy= pt || teta opehexaoctaco tettic = co || bidhin  (wedge ofdottascad)= oct || hexaco= tet || alt. rapacotetaco altepetric = co || tetaf= tet || hexaco= tet || inv tepacotriddipasc = line || perp triddip

ratip = rat || rat    (uniform)scadip = scad || scad (uniform)

icaf = ico || dual icope

rixalspix = rix || inv spix (segment ofscal)scadaspix = scad || spix    (segment ofscal)

ax = pent || pent                   (regular)troctpy = pt || troct               (segment ofbrag)dottaspix = dot || spix             (segment ofbrag)spixa = spix || inv spix            (segment ofbrag)ratanit = rat || nit                (segment ofbrag)hexcopedaw = hex || axis-ortho cope (segment ofbrag)hexaicope = hex || icope            (segment ofbrag)troctal traco = troct || inv. traco

pentanit = pent || nit

spixip = spix || spix         (uniform)ritgyt = rit || gyro rita     (scaliform,                               wedge ofrojak)ritahin = rit || hin          (wedge ofrojak)hinanit = hin || nit          (segment ofrojak)nitasiphin = nit || siphin    (segment ofrojak)ratasiphin = rat || siphin    (segment ofrojak)rixaspix = rix || spix        (segment ofrojak)spixalsarx = spix || inv sarx (segment ofrojak)icarita = ico || rita         (wedge ofrojak)hexaico alrittric = hex || alt. icarit (wedge ofrojak)= ico || hexalrit= rit || alt. hexaicorappippy = pt || rappip       (segment ofrojak)sripaf = srip || srippip

trasrip = srip || srippip (uniform)

tettut = tut || tratut          (uniform)hinasiphin = hin || siphin      (segment ofsochax)siphina = siphin || alt. siphin (segment ofsochax)ritas = rita || alt. rita       (segment ofsiphina)

rixatix = rix || tix (segment ofsril)

siphinnip = siphin || siphin (uniform)

sarxip = sarx || sarx (uniform)

tixip = tix || tix           (uniform)nitarin = nit || rin         (segment ofbrox)rixasarx = rix || sarx       (segment ofbrox)sarxasibrid = sarx || sibrid (segment ofbrox)

pentarin = pent || rin

bittixa = bittix || inv bittix (scaliform)

open = {8} || otet (uniform)

thexgyt = thex || gyro thexa (scaliform,                              wedge ofhejak)hinarin = hin || rin         (segment ofhejak)

cappixa = cappix || alt cappix (scaliform)sirhina = sirhin || alt sirhin (scaliform,                                segment ofsophax)

cardip = card || card        (uniform,                              segment ofram)dottasibrid = dot || sibrid  (segment ofram)sibridacard = sibrid || card (segment ofram)nitasirhin = nit || sirhin   (segment ofram)sirhinasart = sirhin || sart (segment ofram)

thina = thin || alt thin     (scaliform)                              segment ofsirhax)sirhinathin = sirhin || thin (segment ofsirhax)

tahgyt = tah || gyro taha (scaliform,                           wedge ofharjak)rinathin = rin || thin    (segment ofharjak)

sartabittit = sart || bittit        (segment ofsiborg)bittita sibrant = bittit || sibrant (segment ofsiborg)

squagippid = gippiddip || gippiddip (uniform)

gocadip = gocad || gocad (uniform)

gacnetip = gacnet || gacnet (uniform)

(n,pen)-dip = {n} || (n,tet)-dip (uniform)

(n-g, dual n-g, para n-p, gyro n-p) lace simplex

(n,m)-dip || (n,m)-dafup

Somenon-convex segmentopeta would be:

• 0.639069 -ogquithdow = octagram || fully perp. quith
• 0.639240 -stasissiddow = pentagram || fully perp. sissid
• 0.645976 -tiquithdow = triangle || fully perp. quith
• 0.707107 -guhsa = hix || dual pseudo hix
• 0.707107 -starpglassdit =oxoo5/2ooox xooo5/2ooxo&#xr
• 0.845154 -firl = hix || firx

---- 7D----

(Just some) Convex Segmentoexa   (up)

oca = pt || hop        (regular)= line || perp hix= {3} || perp pen= tet || perp tet

zee = hop || inv hop       (regular)geepy = pt || gee          (segment ofzee)taccasc = line || perp tac (lune ofzee)hexete = {3} || perp hex   (wedge ofzee)squix = {4} || perp pen    (wedge ofzee)octepe = tet || perp oct   (wedge ofzee)

hopip = hop || hop (uniform)

roc = hop || ril                (uniform)hixippy = pt || hixip           (segment ofroc)trialtrapen = {3} || inv trapen (segment ofroc)octatetdip = oct || tetdip      (segment ofroc)rapatrapen = rap || trapen      (segment ofroc)rixahixip = rix || hixip        (segment ofroc)tedroc = tedrix || hixip        (segment ofroc)geep = gee || gee               (uniform)= hixip || inv hixiptacpyp = line || taccup         (segment ofgeep)trahix = hix || hixip           (uniform,                                 wedge ofnaq)rila = ril || alt. ril          (scaliform,                                 segment ofnaq)jaka = jak || alt. jak          (scaliform,                                 segment ofnaq)jakpy = pt || jak               (segment ofnaq)dijakpy = pt || dijak           (segment ofnaq)hixaf = hix || inv hixip        (segment ofnaq)hopalril = hop || inv ril       (segment ofnaq)gahax = gee || hax              (segment ofnaq)hinsc = line || perp hin        (wedge ofnaq)hexalhax = hex || alt. hax      (wedge ofnaq)trapendafup = trapen || bidual trapen (scaliform)rapete = {3} || perp raptrippepe = trip || perp tet

tratac = tac || taccup (uniform)

hesa = hax || gyro hax                    (uniform)rilpy = pt || ril                         (segment ofhesa)hexal trahex = hex || gyro trahex         (segment ofhesa)hopabril = hop || bril                    (segment ofhesa)rilalbril = ril || alt. bril              (segment ofhesa)hinaf = hin || alt. hinnip                (segment ofhesa)trahex dafup = trahex || dual-gyro trahex (segment ofhesa)tetal tetdip = tet || dual tetdiptethex = hex || trahex                    (uniform)= tetdip || para-dual tetdip= hexip || lacing-ortho hexippenpasc = line || perp penptridafupap = tridafup || lacing-ortho tridafup (scaliform)

squahix = hixip || hixip (uniform)jakip = jak || jak       (uniform)

broc = ril || bril               (uniform)rapaltrarap = rap || alt. trarap (segment ofbroc)tetocta = tetoct || alt. tetoct  (scaliform,                                  segment ofbroc)

trahin = hin || hinnip (uniform)

rillip = ril || ril (uniform)

trippen = trapen || trapen (uniform)

trial trarap = {3} || alt. trarap

he = bril || inv bril       (uniform)tetdippy = pt || tetdip     (segment ofhe)tetdippa octdip = tetdip || octdip     (segment ofhe)trarapdafup = trarap || bi-alt. trarap (segment ofhe)trapen altralrap = trapen || bi-alt. trarapsquarat = ratip || ratip    (uniform)                             diminishing ofbarz)tettepe = tetdip || tetdip  (uniform)trarix = rix || rixip       (uniform,                             wedge oflaq)haxpy = pt || hax           (segment oflaq)haxarag = hax || rag        (segment oflaq)jakamo = jak || mo          (segment oflaq)hopalbril = hop || inv bril (segment oflaq)brilastaf = bril || staf    (segment oflaq)taccuppy = pt || taccup     (segment ofrez)garag = gee || rag          (segment ofrez)rilastaf = ril || staf      (segment ofrez)hopastaf = hop || staf      (segment ofsuph                             diminishing oflaq)rixasc = line || perp rixrixaf = rix || inv rixiptrial trahex = {3} || inv trahextrahex aico = trahex || icoratahinnip = rat || hinnip

titridafup = trittip || bidual trittip (scaliform)rixap = rixip || inv rixip             (scaliform)

brillip = bril || bril (uniform)

haxip = hax || hax (uniform)

tratratrip = trittip || trittip (uniform)stafip = staf || staf           (uniform)hinnipa ratip = hinnip || ratip

trarat = rat || ratip (uniform)

trahexpy = pt || trahex  (segment ofbarz)ragabrag = rag || brag   (segment ofbarz)scala = scal || inv scal (scaliform,                          segment ofbarz)

hept = ax || ax                   (regular)brilalspil = bril || inv spil     (segment ofsco)scala spil = scal || spil         (segment ofsco)cubico = squico || squico         (uniform,                                   segment oflin)rojaka = rojak || alt. rojak      (scaliform,                                   segment oflin)haxabrag = hax || brag            (segment oflin)haxa cytedbrag = hax || cytedbrag (segment oflin)moarojak = mo || rojak            (segment oflin)bragasochax = brag || sochax      (segment oflin)brilpy = pt || bril               (segment oflin)hinaratip = hin || ratip          (segment oflin)spila = spil || inv spil          (scaliform)

rojakip = rojak || rojak (uniform)

trasarx = sarx || sarxip   (uniform)bragabrox = brag || brox   (segment ofsez)ragasochax = rag || sochax (segment ofranq)jakarojak = jak || rojak   (segment ofranq)rojakatrim = rojak || trim (segment ofranq)

srillip = sril || sril (uniform)

ohix = {8} || open (uniform)

broxarax = brox || rax          (segment ofbersa)sabrila = sabril || inv. sabril (scaliform)

jakatrim = jak || trim       (segment ofstanq)hejaka = hejak || alt. hejak (segment ofstanq)

haxabrox = hax || brox        (segment ofrolaq)broxa sophax = brox || sophax (segment ofrolaq)rojaka hejak = rojak || hejak (segment ofrolaq)

crala = cral || inv. cral          (scaliform)shopjaka = shopjak || alt. shopjak (scaliform,                                    segment ofbranq)

thaxa = thax || alt. thax (scaliform,                           segment ofsirhesa)

hagippiddip = hagippid || hagippid (uniform)

gotafip = gotaf || gotaf (uniform)

gopamp = gopam || gopam (uniform)

n,n,n-tippip = n,n,n-tip || n,n,n-tip (uniform)

(n,m)-dafupap = (n,m)-dafup || lacing-ortho (n,m)-dafup (scaliform)

Somenon-convex segmentoexa would be:

• 0.646447 -quithdow = quith || fully perp. quith (aka: quith disphenoid)
• 0.831254 -sissiddow = sissid || fully perp. sissid (aka: sissid disphenoid)

---- 8D----

(Just some) Convex Segmentozetta   (up)

ene  = pt || oca (regular)

ek  = oca || dual oca      (regular)zeepy  = pt || zee         (segment ofek)geeasc = line || perp gee (wedge ofek)= pt || geepytaccete = {3} || perp tac (wedge ofek)        = line || perp tacpy        = pt || taccaschexepe = tet || perp hex (lune ofek)       = {3} || perp hexpy       = line || perp hexasc       = pt || hexete

ocpe  = oca || oca (uniform)

zeep  = zee || zee (uniform)

trihop  = hop || hopip (uniform)

rene  = oca || roc (uniform)

pendip  = pen || tetpen (uniform)

penhex = hex || tethex (uniform)       = hexip || trahex       = tetpen || first-dual tetpen

octhix = oct || octpen (uniform)       = ope || tetoct       = trahix || first-dual trahix

squahop  = hopip || hopip (uniform)

trajak = jak || jakip        (uniform,                              wedge offy)brene  = roc || broc          (uniform,                              segment offy)hocto  = hesa || gyro hesa    (uniform,                              segment offy)penrap = rap || tetrap       (uniform,= rappip || trarap     segment offy)= tetpen || octpentriphix  = trahix || trahix   (uniform)tethin  = hin || trahin       (uniform)rocip  = roc || roc           (uniform)rocpy  = pt || roc            (segment ofhocto)rocahe = roc || he           (segment ofhocto)ocabroc = oca || broc        (segment ofhocto)broca = broc || inv broc     (scaliform,                              segment ofhocto)ocasuph = oca || suph        (segment ofsoxeb)naqpy = pt || naq            (segment offy)jakapy = pt || jaka          (wedge offy)jakaf = jak || alt. jakip    (wedge offy)jakap = jaka || jaka         (scaliform,                              segment offy)naqalaq = naq || laq         (segment offy)naqpe  = naq || naq           (uniform,                              segment offy)zahesa = zee || hesa         (segment offy)hesa arez = hesa || rez      (segment offy)ocalroc  = oca || inv roc     (segment offy)rocalbroc  = roc || inv broc  (segment offy)rocasuph  = roc || suph       (segment offy)hexal hesa  = hex || alt hesa (wedge ofcodify)zarez = zee || rez           (segment ofrek)octa tethex  = oct || tethextethex aico  = tethex || icorapepe = tet || perp rap

tetrappal octrap = tetrap || alt. octrap

laqpe  = laq || laq (uniform)

rezabarz = rez || barz (segment ofbark)

octo  = hept || hept              (regular)trarojak = rojak || rojakip      (uniform)barzasez = barz || sez           (segment oftark)hesapy  = pt || hesa              (segment ofbay)laqalin  = laq || lin             (segment ofbay)linaranq  = lin || ranq           (segment ofbay)rojakaf = rojak || alt rojakip   (segment ofbay)rojakap = rojakip || alt rojakip (segment ofbay)= rojaka || rojaka

---- 9D----

(Just some) Convex Segmentoyotta   (up)

day = pt || ene (regular)

vee = ene || dual ene (regular)

enep = ene || ene (uniform)

ekip = ek || ek (uniform)

trioc = oca || ocpe (uniform)

reday = ene || rene (uniform)

penhix = hix || tethix (uniform)= pen || pendip

squoc = ocpe || ocpe (uniform)

breday = rene || brene (uniform)

henne = hocto || gyro hocto (uniform)

treday = brene || trene (uniform)

rapdafup = rapdip || bi-alt. rapdip (scaliform)

enne = octo || octo (regular)

----- 10D-----

(Just some) Convex Segmentoxenna   (up)

ux = pt || day (regular)

ka = day || dual day (regular)

ru = day || reday (uniform)

bru = reday || breday (uniform)

tru = breday || treday (uniform)