Uh oh!
There was an error while loading.Please reload this page.
- Notifications
You must be signed in to change notification settings - Fork102
💪 Models' quality and performance metrics (R2, ICC, LOO, AIC, BF, ...)
License
easystats/performance
Folders and files
| Name | Name | Last commit message | Last commit date | |
|---|---|---|---|---|
Repository files navigation
Test if your model is a good model!
A crucial aspect when building regression models is to evaluate thequality of modelfit. It is important to investigate how well models fitto the data and which fit indices to report. Functions to creatediagnostic plots or to compute fit measures do exist, however, mostlyspread over different packages. There is no unique and consistentapproach to assess the model quality for different kind of models.
The primary goal of theperformance package is to fill this gap andto provide utilities for computingindices of model quality andgoodness of fit. These include measures like r-squared (R2), rootmean squared error (RMSE) or intraclass correlation coefficient (ICC) ,but also functions to check (mixed) models for overdispersion,zero-inflation, convergence or singularity.
Theperformance package is available on CRAN, while its latestdevelopment version is available on R-universe (fromrOpenSci).
| Type | Source | Command |
|---|---|---|
| Release | CRAN | install.packages("performance") |
| Development | R-universe | install.packages("performance", repos = "https://easystats.r-universe.dev") |
Once you have downloaded the package, you can then load it using:
library("performance")Tip
Instead of
library(performance), uselibrary(easystats). This willmake all features of the easystats-ecosystem available.To stay updated, use
easystats::install_latest().
To cite performance in publications use:
citation("performance")#> To cite package 'performance' in publications use:#>#> Lüdecke et al., (2021). performance: An R Package for Assessment, Comparison and#> Testing of Statistical Models. Journal of Open Source Software, 6(60), 3139.#> https://doi.org/10.21105/joss.03139#>#> A BibTeX entry for LaTeX users is#>#> @Article{,#> title = {{performance}: An {R} Package for Assessment, Comparison and Testing of Statistical Models},#> author = {Daniel Lüdecke and Mattan S. Ben-Shachar and Indrajeet Patil and Philip Waggoner and Dominique Makowski},#> year = {2021},#> journal = {Journal of Open Source Software},#> volume = {6},#> number = {60},#> pages = {3139},#> doi = {10.21105/joss.03139},#> }
There is a nice introduction into the package onyoutube.
performance has a genericr2() function, which computes ther-squared for many different models, including mixed effects andBayesian regression models.
r2() returns a list containing values related to the “mostappropriate” r-squared for the given model.
model<- lm(mpg~wt+cyl,data=mtcars)r2(model)#> # R2 for Linear Regression#> R2: 0.830#> adj. R2: 0.819model<- glm(am~wt+cyl,data=mtcars,family=binomial)r2(model)#> # R2 for Logistic Regression#> Tjur's R2: 0.705library(MASS)data(housing)model<- polr(Sat~Infl+Type+Cont,weights=Freq,data=housing)r2(model)#> Nagelkerke's R2: 0.108
The different R-squared measures can also be accessed directly viafunctions liker2_bayes(),r2_coxsnell() orr2_nagelkerke() (see afull list of functionshere).
For mixed models, theconditional andmarginal R-squared arereturned. Themarginal R-squared considers only the variance of thefixed effects and indicates how much of the model’s variance isexplained by the fixed effects part only. Theconditional R-squaredtakes both the fixed and random effects into account and indicates howmuch of the model’s variance is explained by the “complete” model.
For frequentist mixed models,r2() (resp.r2_nakagawa()) computesthemean random effect variances, thusr2() is also appropriate formixed models with more complex random effects structures, like randomslopes or nested random effects (Johnson 2014; Nakagawa, Johnson, andSchielzeth 2017).
set.seed(123)library(rstanarm)model<- stan_glmer(Petal.Length~Petal.Width+ (1|Species),data=iris,cores=4)r2(model)#> # Bayesian R2 with Compatibility Interval#>#> Conditional R2: 0.954 (95% CI [0.951, 0.957])#> Marginal R2: 0.414 (95% CI [0.204, 0.644])library(lme4)model<- lmer(Reaction~Days+ (1+Days|Subject),data=sleepstudy)r2(model)#> # R2 for Mixed Models#>#> Conditional R2: 0.799#> Marginal R2: 0.279
Similar to R-squared, the ICC provides information on the explainedvariance and can be interpreted as “the proportion of the varianceexplained by the grouping structure in the population” (Hox 2010).
icc() calculates the ICC for various mixed model objects, includingstanreg models.
library(lme4)model<- lmer(Reaction~Days+ (1+Days|Subject),data=sleepstudy)icc(model)#> # Intraclass Correlation Coefficient#>#> Adjusted ICC: 0.722#> Unadjusted ICC: 0.521
…and models of classbrmsfit.
library(brms)set.seed(123)model<- brm(mpg~wt+ (1|cyl)+ (1+wt|gear),data=mtcars)
icc(model)#> # Intraclass Correlation Coefficient#>#> Adjusted ICC: 0.930#> Unadjusted ICC: 0.771
Overdispersion occurs when the observed variance in the data is higherthan the expected variance from the model assumption (for Poisson,variance roughly equals the mean of an outcome).check_overdispersion() checks if a count model (including mixedmodels) is overdispersed or not.
library(glmmTMB)data(Salamanders)model<- glm(count~spp+mined,family=poisson,data=Salamanders)check_overdispersion(model)#> # Overdispersion test#>#> dispersion ratio = 2.946#> Pearson's Chi-Squared = 1873.710#> p-value = < 0.001
Overdispersion can be fixed by either modelling the dispersion parameter(not possible with all packages), or by choosing a differentdistributional family (like Quasi-Poisson, or negative binomial, see(Gelman and Hill 2007)).
Zero-inflation (in (Quasi-)Poisson models) is indicated when the amountof observed zeros is larger than the amount of predicted zeros, so themodel isunderfitting zeros. In such cases, it is recommended to usenegative binomial or zero-inflated models.
Usecheck_zeroinflation() to check if zero-inflation is present in thefitted model.
model<- glm(count~spp+mined,family=poisson,data=Salamanders)check_zeroinflation(model)#> # Check for zero-inflation#>#> Observed zeros: 387#> Predicted zeros: 298#> Ratio: 0.77
A “singular” model fit means that some dimensions of thevariance-covariance matrix have been estimated as exactly zero. Thisoften occurs for mixed models with overly complex random effectsstructures.
check_singularity() checks mixed models (of classlme,merMod,glmmTMB orMixMod) for singularity, and returnsTRUE if the modelfit is singular.
library(lme4)data(sleepstudy)# prepare dataset.seed(123)sleepstudy$mygrp<- sample(1:5,size=180,replace=TRUE)sleepstudy$mysubgrp<-NAfor (iin1:5) {filter_group<-sleepstudy$mygrp==isleepstudy$mysubgrp[filter_group]<- sample(1:30,size= sum(filter_group),replace=TRUE)}# fit strange modelmodel<- lmer(Reaction~Days+ (1|mygrp/mysubgrp)+ (1|Subject),data=sleepstudy)check_singularity(model)#> [1] TRUE
Remedies to cure issues with singular fits can be foundhere.
Linear models assume constant error variance (homoskedasticity).
Thecheck_heteroscedasticity() functions assess if this assumption hasbeen violated:
data(cars)model<- lm(dist~speed,data=cars)check_heteroscedasticity(model)#> Warning: Heteroscedasticity (non-constant error variance) detected (p = 0.031).
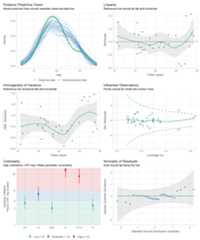
performance provides many functions to check model assumptions, likecheck_collinearity(),check_normality() orcheck_heteroscedasticity(). To get a comprehensive check, usecheck_model().
# defining a modelmodel<- lm(mpg~wt+am+gear+vs*cyl,data=mtcars)# checking model assumptionscheck_model(model)
model_performance() computes indices of model performance forregression models. Depending on the model object, typical indices mightbe r-squared, AIC, BIC, RMSE, ICC or LOOIC.
m1<- lm(mpg~wt+cyl,data=mtcars)model_performance(m1)#> # Indices of model performance#>#> AIC | AICc | BIC | R2 | R2 (adj.) | RMSE | Sigma#> ---------------------------------------------------------------#> 156.010 | 157.492 | 161.873 | 0.830 | 0.819 | 2.444 | 2.568
m2<- glm(vs~wt+mpg,data=mtcars,family="binomial")model_performance(m2)#> # Indices of model performance#>#> AIC | AICc | BIC | Tjur's R2 | RMSE | Sigma | Log_loss | Score_log | Score_spherical | PCP#> -----------------------------------------------------------------------------------------------------#> 31.298 | 32.155 | 35.695 | 0.478 | 0.359 | 1.000 | 0.395 | -14.903 | 0.095 | 0.743
library(lme4)m3<- lmer(Reaction~Days+ (1+Days|Subject),data=sleepstudy)model_performance(m3)#> # Indices of model performance#>#> AIC | AICc | BIC | R2 (cond.) | R2 (marg.) | ICC | RMSE | Sigma#> ----------------------------------------------------------------------------------#> 1755.628 | 1756.114 | 1774.786 | 0.799 | 0.279 | 0.722 | 23.438 | 25.592
Thecompare_performance() function can be used to compare theperformance and quality of several models (including models of differenttypes).
counts<- c(18,17,15,20,10,20,25,13,12)outcome<- gl(3,1,9)treatment<- gl(3,3)m4<- glm(counts~outcome+treatment,family= poisson())compare_performance(m1,m2,m3,m4,verbose=FALSE)#> # Comparison of Model Performance Indices#>#> Name | Model | AIC (weights) | AICc (weights) | BIC (weights) | RMSE | Sigma | Score_log#> -----------------------------------------------------------------------------------------------#> m1 | lm | 156.0 (<.001) | 157.5 (<.001) | 161.9 (<.001) | 2.444 | 2.568 |#> m2 | glm | 31.3 (>.999) | 32.2 (>.999) | 35.7 (>.999) | 0.359 | 1.000 | -14.903#> m3 | lmerMod | 1764.0 (<.001) | 1764.5 (<.001) | 1783.1 (<.001) | 23.438 | 25.592 |#> m4 | glm | 56.8 (<.001) | 76.8 (<.001) | 57.7 (<.001) | 3.043 | 1.000 | -2.598#>#> Name | Score_spherical | R2 | R2 (adj.) | Tjur's R2 | Log_loss | PCP | R2 (cond.) | R2 (marg.)#> ---------------------------------------------------------------------------------------------------#> m1 | | 0.830 | 0.819 | | | | |#> m2 | 0.095 | | | 0.478 | 0.395 | 0.743 | |#> m3 | | | | | | | 0.799 | 0.279#> m4 | 0.324 | | | | | | |#>#> Name | ICC | Nagelkerke's R2#> ------------------------------#> m1 | |#> m2 | |#> m3 | 0.722 |#> m4 | | 0.657
One can also easily compute and acompositeindexof model performance and sort the models from the best one to the worse.
compare_performance(m1,m2,m3,m4,rank=TRUE,verbose=FALSE)#> # Comparison of Model Performance Indices#>#> Name | Model | RMSE | Sigma | AIC weights | AICc weights | BIC weights | Performance-Score#> -----------------------------------------------------------------------------------------------#> m2 | glm | 0.359 | 1.000 | 1.000 | 1.000 | 1.000 | 100.00%#> m4 | glm | 3.043 | 1.000 | 2.96e-06 | 2.06e-10 | 1.63e-05 | 37.67%#> m1 | lm | 2.444 | 2.568 | 8.30e-28 | 6.07e-28 | 3.99e-28 | 36.92%#> m3 | lmerMod | 23.438 | 25.592 | 0.00e+00 | 0.00e+00 | 0.00e+00 | 0.00%
Finally, we provide convenient visualisation (thesee package must beinstalled).
plot(compare_performance(m1,m2,m4,rank=TRUE,verbose=FALSE))
test_performance() (andtest_bf, its Bayesian sister) carries outthe most relevant and appropriate tests based on the input (forinstance, whether the models are nested or not).
set.seed(123)data(iris)lm1<- lm(Sepal.Length~Species,data=iris)lm2<- lm(Sepal.Length~Species+Petal.Length,data=iris)lm3<- lm(Sepal.Length~Species*Sepal.Width,data=iris)lm4<- lm(Sepal.Length~Species*Sepal.Width+Petal.Length+Petal.Width,data=iris)test_performance(lm1,lm2,lm3,lm4)#> Name | Model | BF | Omega2 | p (Omega2) | LR | p (LR)#> ------------------------------------------------------------#> lm1 | lm | | | | |#> lm2 | lm | > 1000 | 0.69 | < .001 | -6.25 | < .001#> lm3 | lm | > 1000 | 0.36 | < .001 | -3.44 | < .001#> lm4 | lm | > 1000 | 0.73 | < .001 | -7.77 | < .001#> Each model is compared to lm1.test_bf(lm1,lm2,lm3,lm4)#> Bayes Factors for Model Comparison#>#> Model BF#> [lm2] Species + Petal.Length 3.45e+26#> [lm3] Species * Sepal.Width 4.69e+07#> [lm4] Species * Sepal.Width + Petal.Length + Petal.Width 7.58e+29#>#> * Against Denominator: [lm1] Species#> * Bayes Factor Type: BIC approximation
Plotting functions are available through theseepackage.
Please note that the performance project is released with aContributorCode ofConduct.By contributing to this project, you agree to abide by its terms.
We are happy to receive bug reports, suggestions, questions, and (mostof all) contributions to fix problems and add features.
Please follow contributing guidelines mentioned here:
https://easystats.github.io/performance/CONTRIBUTING.html
Gelman, Andrew, and Jennifer Hill. 2007.Data Analysis Using Regressionand Multilevel/Hierarchical Models. Analytical Methods for SocialResearch. Cambridge ; New York: Cambridge University Press.
Hox, J. J. 2010.Multilevel Analysis: Techniques and Applications. 2nded. Quantitative Methodology Series. New York: Routledge.
Johnson, Paul C. D. 2014. “Extension of Nakagawa & Schielzeth’s R2 GLMMto Random Slopes Models.” Edited by Robert B. O’Hara.Methods inEcology and Evolution 5 (9): 944–46.
Nakagawa, Shinichi, Paul C. D. Johnson, and Holger Schielzeth. 2017.“The Coefficient of Determination R2 and Intra-Class CorrelationCoefficient from Generalized Linear Mixed-Effects Models Revisited andExpanded.”Journal of The Royal Society Interface 14 (134): 20170213.
About
💪 Models' quality and performance metrics (R2, ICC, LOO, AIC, BF, ...)
Topics
Resources
License
Code of conduct
Contributing
Uh oh!
There was an error while loading.Please reload this page.
Stars
Watchers
Forks
Sponsor this project
Uh oh!
There was an error while loading.Please reload this page.
Packages0
Uh oh!
There was an error while loading.Please reload this page.