Folders and files

Name		Name	Last commit message	Last commit date
Latest commit History 447 Commits
.github		.github
docs		docs
joss		joss
src		src
test		test
.JuliaFormatter.toml		.JuliaFormatter.toml
.gitignore		.gitignore
.typos.toml		.typos.toml
CITATION.bib		CITATION.bib
LICENSE		LICENSE
Project.toml		Project.toml
README.md		README.md

Repository files navigation

GlobalSensitivity.jl

GlobalSensitivity.jl package contains implementation of some the most popular GSA methods. Currently it supports Delta Moment-Independent, DGSM, EASI, eFAST, Morris, Mutual Information, Fractional Factorial, RBD-FAST, RSA, Sobol and Regression based sensitivity methods.

Tutorials and Documentation

For information on using the package,see the stable documentation. Use thein-development documentation for the version ofthe documentation, which contains the unreleased features.

Installation

The GlobalSensitivity.jl package can be installed with julia's package manager as shown below:

using PkgPkg.add("GlobalSensitivity")

General Interface

The general interface for performing global sensitivity analysis using this package is:

res=gsa(f, method, param_range; samples, batch=false)

Example

Sobol method on theIshigami function.

Serial execution

functionishi(X)    A=7    B=0.1sin(X[1])+ A*sin(X[2])^2+ B* X[3]^4*sin(X[1])endn=600000lb=-ones(4)* πub=ones(4)* πsampler=SobolSample()A, B= QuasiMonteCarlo.generate_design_matrices(n, lb, ub, sampler)res1=gsa(ishi,Sobol(order= [0,1,2]), A, B)

Using batching interface

functionishi_batch(X)    A=7    B=0.1@.sin(X[1, :])+ A*sin(X[2, :])^2+ B* X[3, :]^4*sin(X[1, :])endres2=gsa(ishi_batch,Sobol(), A, B, batch=true)

Regression based and Morris method sensitivity analysis of Lotka Volterra model.

using GlobalSensitivity, QuasiMonteCarlo, OrdinaryDiffEq, Statistics, CairoMakiefunctionf(du, u, p, t)    du[1]= p[1]* u[1]- p[2]* u[1]* u[2]#prey    du[2]=-p[3]* u[2]+ p[4]* u[1]* u[2]#predatorendu0= [1.0;1.0]tspan= (0.0,10.0)p= [1.5,1.0,3.0,1.0]prob=ODEProblem(f, u0, tspan, p)t=collect(range(0, stop=10, length=200))f1=function (p)    prob1=remake(prob; p= p)    sol=solve(prob1,Tsit5(); saveat= t)return [mean(sol[1, :]),maximum(sol[2, :])]endbounds= [[1,5], [1,5], [1,5], [1,5]]reg_sens=gsa(f1,RegressionGSA(true), bounds)fig=Figure(resolution= (600,400))ax,hm= CairoMakie.heatmap(fig[1,1], reg_sens.partial_correlation,    figure= (resolution= (300,200),),    axis= (xticksvisible=false,        yticksvisible=false,        yticklabelsvisible=false,        xticklabelsvisible=false,        title="Partial correlation"))Colorbar(fig[1,2], hm)ax,hm= CairoMakie.heatmap(fig[2,1], reg_sens.standard_regression,    figure= (resolution= (300,200),),    axis= (xticksvisible=false,        yticksvisible=false,        yticklabelsvisible=false,        xticklabelsvisible=false,        title="Standard regression"))Colorbar(fig[2,2], hm)fig

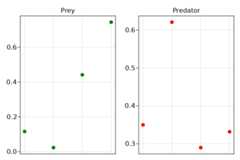
using StableRNGs_rng=StableRNG(1234)morris_sens=gsa(f1,Morris(), bounds, rng= _rng)fig=Figure(resolution= (300,200))scatter(fig[1,1], [1,2,3,4], morris_sens.means_star[1, :],    color=:green, axis= (xticksvisible=false,        xticklabelsvisible=false, title="Prey (Morris)"))scatter(fig[1,2], [1,2,3,4], morris_sens.means_star[2, :],    color=:red, axis= (xticksvisible=false,        xticklabelsvisible=false, title="Predator (Morris)"))fig

Citing

If you use this software in your work, please cite:

@article{dixit2022globalsensitivity,title={GlobalSensitivity. jl: Performant and Parallel Global Sensitivity Analysis with Julia},author={Dixit, Vaibhav Kumar and Rackauckas, Christopher},journal={Journal of Open Source Software},volume={7},number={76},pages={4561},year={2022}}