Movatterモバイル変換

Theordgam R-package

Theordgam package enables to fit an additiveproportional odds model to ordinal data.

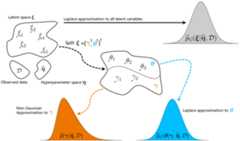
The combination ofLaplace approximations and ofBayesian P-splines (namedLPS) enable fast andflexible inference in a Bayesian framework. The Gaussian Markov randomfield prior assumed for the penalized spline parameters and theBernstein-von Mises theorem typically provide reliable Laplaceapproximation to the posterior distribution of these quantities.However, this accuracy can be seriously compromised for some unpenalizedparameters, especially when the information synthesized by the prior andthe likelihood is sparse.

We propose a refined version of the LPS methodology by splitting theparameter space in two subsets,\(\pmb{\zeta}=(\pmb{\gamma}^\top,\pmb{\theta}^\top)^\top\). The first set involves the non-penalized parameters\(\pmb{\gamma}\) for which the jointposterior distribution\(p(\pmb{\gamma}|\pmb{\lambda},{\cal D})\) isapproached from a non-Gaussian perspective with an approximation schemetailored to capture asymmetry and kurtosis, while the conditionalposterior distribution\(p(\pmb{\theta}|\pmb{\gamma},\pmb{\lambda},{\calD})\) for the penalized parameters\(\pmb{\theta}\) in the complementary setundergoes the LPS treatment with Laplace approximations, see Fig.1 (with\(\pmb{\eta}=\pmb{\lambda}\)).

The marginal posterior density\(p(\pmb{\nu}|{\cal D})\) for the log of thepenalty parameters,\(\pmb{\nu}=\log(\pmb{\lambda})\), also couldbe approximated using a product of skew-t densities. More details can befound in Lambert & Gressani (2023)[1].

Theordgam package inaction

Let us illustrate the use of theordgam package on a datasubset (\(n=552\)) from the EuropeanSocial Survey (ESS 2018) specific to the French speaking respondentsfrom Wallonia, one of the three regions in Belgium. Each of theparticipants (aged at least 15) was asked to react to the followingstatement,Gay men and lesbians should be free to live their ownlife as they wish, with a positioning on a Likert scale going from1 (Agree strongly) to 5 (Disagree strongly).

## Package installation and loading## install.packages("devtools")## devtools::install_github("plambertULiege/ordgam")library(ordgam)## Data readingdata(freehmsDataBE)donnees=subset(freehmsDataBE,region=="WAL")## Focus on Walloniahead(donnees)

##    freehms   gndr age eduyrs region## 2        1   Male  25     17    WAL## 3        2 Female  76      6    WAL## 7        1   Male  69     17    WAL## 9        2   Male  36     10    WAL## 12       1   Male  54      7    WAL## 18       1 Female  28     14    WAL

Model fitting

Let us fit a proportional odds model to these data with the number ofcompleted years of education (\(14.1\pm4.4\) years) and age (\(47.3\pm18.5\) years) entering as additive terms,\(L=10\) recentered B-splines spanning eachcovariate range, and Gamma priors for the penalty parameters,\(\lambda_j\sim{\cal G}(1,10^{-4})\) (\(j=1,2\)).

## Model fit with a Gamma prior for the penalty parametersmod=ordgam(freehms~s(eduyrs)+s(age),data=donnees,descending =FALSE)print(mod)

## Call:##  ordgam(formula = freehms ~ s(eduyrs) + s(age), data = donnees,      descending = FALSE) ## ## Prior set on the regression paramaters <beta>## ## Parameter estimation:##       est      se     low      up     Z   Pval    ## 1  0.0272  0.1152 -0.1986  0.2530  0.24   0.81    ## 2  1.6318  0.1400  1.3574  1.9062 11.66 <2e-16 ***## 3  2.5509  0.1863  2.1858  2.9160 13.69 <2e-16 ***## 4  4.4168  0.4163  3.6008  5.2328 10.61 <2e-16 ***## ## Approximate significance of smooth terms:##            edf    Tr     Pval  Chi2    Pval    ## f(eduyrs) 1.24  1.01 0.477617  1.15 0.35501    ## f(age)    2.55 18.77 0.000265 18.82 0.00017 ***## ## Selected penalty parameters <lambda>:  191.7967 18.40125 ## Lambda log prior:  dgamma(lambda, 1, 1e-04, log = TRUE)## ## Likelihood - Information criterions (n = 552):##      edf     logL logLmarg      AIC      BIC ##     7.79  -598.66  -606.75  1212.90  1246.49 ## ## NOTE: model the odds of a response value in the lower scale

The estimated additive terms can also be visualized:

plot(mod,mfrow=c(1,2))

model= mod## Model for which the approximation is required## Skew-t approximation to the marginal of gamma.tilde[k]ngamma=with(model, nalpha+nfixed)## Number of non-penalized parmsgamt.ST=list()## Skew-t coefs --> dst(x,dp=coef)for (kin1:ngamma){## Loop over the gamma.tilde components     x.grid=seq(-4,4,length=10)## Grid of values for gamma.tilde[k]     lfy.grid= ordgam::lmarg.gammaTilde(x.grid,k=k,model)## log p(gamma.tilde[k] | D)     gamt.ST[[k]]= ordgam:::STapprox(x.grid,lfy.grid)$dp## Approximate using a skew-t}## Visualization of the posterior for <gamma.tilde[k]>par(mfrow=c(2,2),mar=c(4,5,1,1))for (kin1:ngamma){## Loop over the gamma.tilde components     xlab=bquote(tilde(gamma)[.(k)])     ylab=bquote(p(tilde(gamma)[.(k)]~"|"~lambda~","~D))     xlim= sn::qst(c(.0001,.9999),dp=gamt.ST[[k]])curve(sn::dst(x,dp=gamt.ST[[k]]),xlim=xlim,xlab=xlab,ylab=ylab,col="blue",lwd=2,lty=1)}

## Sampling <gamma.tilde> using the (approximate) independence of its componentsM=10000sample.tilde=matrix(nrow=M,ncol=ngamma)for (kin1:ngamma){## ... or using skew-t approximation    sample.tilde[,k]=c(sn::rst(M,dp=gamt.ST[[k]]))}## Revert sample to the original <gamma> parametrizationgam.hat= model$theta[1:ngamma]## MAP estimateSig= model$Sigma.theta[1:ngamma,1:ngamma]## Variance-covariancesv=svd(Sig) ; V= sv$u ; omega= sv$d## SVDsample.gam=t(gam.hat+ V%*% (sqrt(omega)*t(sample.tilde)))## Skew-t approximation to the marginal of gam[k]gam.ST= gam.ST2=list()for (kin1:ngamma){    temp=hist(sample.gam[,k],plot=FALSE)    gam.ST[[k]]= ordgam:::STapprox(temp$mids,log(temp$density+1e-6))$dp## temp = selm(sample.gam[,k] ~ 1, family="ST")## gam.ST2[[k]] = coef(temp,"DP")}## Visualize p(gamma[k] | lambda,data)par(mfrow=c(2,2),mar=c(4,5,1,1))for (kin1:ngamma){    xlab=bquote(gamma[.(k)])    ylab=bquote(p(gamma[.(k)]~"|"~lambda~","~D))    xlim= sn::qst(c(.0001,.9999),dp=gam.ST[[k]])curve(sn::dst(x,dp=gam.ST[[k]]),lwd=2,col="blue",xlim=xlim,xlab=xlab,ylab=ylab)}

## Model fit with a Gamma prior for the penalty parametersmod.FL=ordgam(freehms~s(eduyrs)+s(age),data=subset(freehmsDataBE,region=="FL"),descending =FALSE)print(mod.FL)

## Call:##  ordgam(formula = freehms ~ s(eduyrs) + s(age), descending = FALSE,##         data = subset(freehmsDataBE, region == "FL")) ## ## Prior set on the regression paramaters <beta>## ## Parameter estimation:##      est     se    low     up     Z    Pval    ## 1 0.3176 0.0866 0.1479 0.4872  3.67 0.00024 ***## 2 2.7105 0.1367 2.4426 2.9784 19.83 < 2e-16 ***## 3 3.4898 0.1829 3.1312 3.8484 19.08 < 2e-16 ***## 4 4.8852 0.3407 4.2174 5.5530 14.34 < 2e-16 ***## ## Approximate significance of smooth terms:##            edf   Tr     Pval Chi2    Pval    ## f(eduyrs) 1.15 27.7 9.64e-07 29.0 1.0e-07 ***## f(age)    2.57 34.6 1.41e-06 34.6 7.9e-08 ***## ## Selected penalty parameters <lambda>:  296.6694 33.87409 ## Lambda log prior:  dgamma(lambda, 1, 1e-04, log = TRUE)## ## Likelihood - Information criterions (n = 1046):##      edf     logL logLmarg      AIC      BIC ##     7.72  -923.13  -932.09  1861.70  1899.94 ## ## NOTE: model the odds of a response value in the lower scale

fhat.FL=plot(mod.FL,mfrow=c(1,2))

model= mod.FL## log(lambda) marginal posteriorspar(mfrow=c(1,2),mar=c(4,5,3,1))for (jin1:2){## Loop over <nu> components## Plot of the approximating skew-t to the marginal posterior of <nu[j]>  xlims= sn::qst(c(.001,.999),dp=model$nu.dp[[j]])  xlab=bquote(log(lambda[.(j)]))  ylab=bquote(p(log(lambda[.(j)])~"|"~D))curve(sn::dst(x,dp=model$nu.dp[[j]]),xlims[1],xlims[2],lwd=2,col="red",main=names(model$lambda)[j],xlab=xlab,ylab=ylab,ylim=c(0,.4))## ... compared to the prior for <nu[j]>curve(exp(model$lprior.lambda(exp(x)))*exp(x),add=T,lty=3,lwd=2)legend("topright",legend=c("Posterior","Prior"),lwd=c(2,2),lty=c(1,3),col=c("red","black"),horiz=TRUE,bty="n",cex=1)}