Movatterモバイル変換

[0]ホーム
URL:

glmtlp:An R Package For Truncated Lasso Penalty

CRAN versiondownloadsR-CMD-check

glmtp icon

Efficient procedures for constrained likelihood estimation withtruncated lasso penalty (Shen et al., 2010; Zhang 2010) for linear andgeneralized linear models.

Note: this is a repo for the version published onCRAN. Please checkchunlinli/glmtlp for newfeatures such as constrained likelihood inference, regression on summarydata, memory efficiency, Gaussian graphical models, and more.

Installation

You can install the released version of glmtlp fromCRAN with:

install.packages("glmtlp")

Examples for GaussianRegression Models

The following are three examples which show you how to useglmtlp to fit gaussian regression models:

library(glmtlp)data("gau_data")colnames(gau_data$X)[gau_data$beta!=0]#> [1] "V1"  "V6"  "V10" "V15" "V20"
# Cross-Validation using TLP penaltycv.fit<-cv.glmtlp(gau_data$X, gau_data$y,family ="gaussian",penalty ="tlp",ncores=2)coef(cv.fit)[abs(coef(cv.fit))>0]#>    intercept           V1           V6          V10          V15          V20#> -0.009678041  1.240223517  0.883202180  0.725708239  1.125994003  0.981402236plot(cv.fit)

cross-validation plot using TLP penalty

# Single Model Fit using TLP penaltyfit<-glmtlp(gau_data$X, gau_data$y,family ="gaussian",penalty ="tlp")coef(fit,lambda = cv.fit$lambda.min)#>    intercept           V1           V2           V3           V4           V5#> -0.009678041  1.240223517  0.000000000  0.000000000  0.000000000  0.000000000#>           V6           V7           V8           V9          V10          V11#>  0.883202180  0.000000000  0.000000000  0.000000000  0.725708239  0.000000000#>          V12          V13          V14          V15          V16          V17#>  0.000000000  0.000000000  0.000000000  1.125994003  0.000000000  0.000000000#>          V18          V19          V20#>  0.000000000  0.000000000  0.981402236predict(fit,X = gau_data$X[1:5, ],lambda = cv.fit$lambda.min)#> [1]  0.1906465  2.2279723 -1.4256042  0.9313886 -2.8152522plot(fit,xvar ="log_lambda",label =TRUE)

solution path plot for single model fit using TLP penalty

# Cross-Validation using L0 penaltycv.fit<-cv.glmtlp(gau_data$X, gau_data$y,family ="gaussian",penalty ="l0",ncores=2)coef(cv.fit)[abs(coef(cv.fit))>0]#>    intercept           V1           V6          V10          V15          V20#> -0.009687042  1.240319880  0.883378583  0.725607300  1.125958218  0.981544178plot(cv.fit)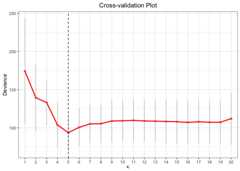

cross-validation plot using L0 penalty

# Single Model Fit using L0 penaltyfit<-glmtlp(gau_data$X, gau_data$y,family ="gaussian",penalty ="l0")coef(fit,kappa = cv.fit$kappa.min)#>    intercept           V1           V2           V3           V4           V5#> -0.009687042  1.240319880  0.000000000  0.000000000  0.000000000  0.000000000#>           V6           V7           V8           V9          V10          V11#>  0.883378583  0.000000000  0.000000000  0.000000000  0.725607300  0.000000000#>          V12          V13          V14          V15          V16          V17#>  0.000000000  0.000000000  0.000000000  1.125958218  0.000000000  0.000000000#>          V18          V19          V20#>  0.000000000  0.000000000  0.981544178predict(fit,X = gau_data$X[1:5, ],kappa = cv.fit$kappa.min)#> [1]  0.190596  2.228306 -1.425994  0.931749 -2.815322plot(fit,xvar ="kappa",label =TRUE)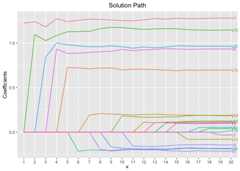

solution path plot for single model fit using L0 penalty

# Cross-Validation using L1 penaltycv.fit<-cv.glmtlp(gau_data$X, gau_data$y,family ="gaussian",penalty ="l1",ncores=2)coef(cv.fit)[abs(coef(cv.fit))>0]#>   intercept          V1          V3          V4          V5          V6#> -0.01185622  1.16222899 -0.06606911 -0.08387185 -0.06870578  0.79106593#>          V8          V9         V10         V11         V14         V15#>  0.01136376  0.01038075  0.62580166  0.10858744  0.08533479  1.04737369#>         V19         V20#> -0.11859786  0.86736897plot(cv.fit)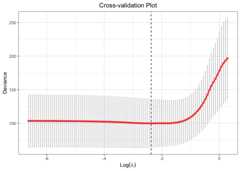

cross-validation plot using L1 penalty

# Single Model Fit using L1 penaltyfit<-glmtlp(gau_data$X, gau_data$y,family ="gaussian",penalty ="l1")coef(fit,lambda = cv.fit$lambda.min)#>   intercept          V1          V2          V3          V4          V5#> -0.01185622  1.16222899  0.00000000 -0.06606911 -0.08387185 -0.06870578#>          V6          V7          V8          V9         V10         V11#>  0.79106593  0.00000000  0.01136376  0.01038075  0.62580166  0.10858744#>         V12         V13         V14         V15         V16         V17#>  0.00000000  0.00000000  0.08533479  1.04737369  0.00000000  0.00000000#>         V18         V19         V20#>  0.00000000 -0.11859786  0.86736897predict(fit,X = gau_data$X[1:5, ],lambda = cv.fit$lambda.min)#> [1]  0.07112074  2.17093497 -1.09936871  0.46108771 -2.25111685plot(fit,xvar ="lambda",label =TRUE)

solution path plot for single model fit using L1 penalty

Examples for LogisticRegression Models

The following are three examples which show you how to useglmtlp to fit logistic regression models:

data("bin_data")colnames(bin_data$X)[bin_data$beta!=0]#> [1] "V1"  "V6"  "V10" "V15" "V20"
# Cross-Validation using TLP penaltycv.fit<-cv.glmtlp(bin_data$X, bin_data$y,family ="binomial",penalty ="tlp",ncores=2)coef(cv.fit)[abs(coef(cv.fit))>0]#>  intercept         V6        V20#> -0.1347141  0.8256183  0.9940325plot(cv.fit)#> Warning: Removed 98 rows containing missing values or values outside the scale range#> (`geom_line()`).#> Warning: Removed 98 rows containing missing values or values outside the scale range#> (`geom_point()`).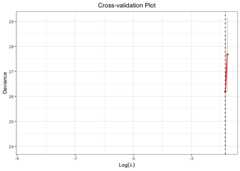

cross-validation plot using TLP penalty for binary data

# Single Model Fit using TLP penaltyfit<-glmtlp(bin_data$X, bin_data$y,family ="binomial",penalty ="tlp")coef(fit,lambda = cv.fit$lambda.min)#>  intercept         V1         V2         V3         V4         V5         V6#> -0.1347141  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.8256183#>         V7         V8         V9        V10        V11        V12        V13#>  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000#>        V14        V15        V16        V17        V18        V19        V20#>  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.9940325predict(fit,X = bin_data$X[1:5, ],type ="response",lambda = cv.fit$lambda.min)#> [1] 0.42562483 0.89838483 0.09767039 0.90898462 0.20822294plot(fit,xvar ="log_lambda",label =TRUE)

solution path plot for single model fit using TLP penalty for binary data

# Cross-Validation using L0 penaltycv.fit<-cv.glmtlp(bin_data$X, bin_data$y,family ="binomial",penalty ="l0",ncores=2)coef(cv.fit)[abs(coef(cv.fit))>0]#>  intercept         V6        V20#> -0.1347137  0.8256471  0.9940180plot(cv.fit)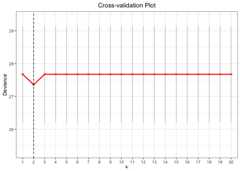

cross-validation plot using L0 penalty for binary data

# Single Model Fit using L0 penaltyfit<-glmtlp(bin_data$X, bin_data$y,family ="binomial",penalty ="l0")coef(fit,kappa = cv.fit$kappa.min)#>  intercept         V1         V2         V3         V4         V5         V6#> -0.1347137  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.8256471#>         V7         V8         V9        V10        V11        V12        V13#>  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000#>        V14        V15        V16        V17        V18        V19        V20#>  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.0000000  0.9940180predict(fit,X = bin_data$X[1:5, ],kappa = cv.fit$kappa.min)#> [1] -0.2996886  2.1793764 -2.2234461  2.3012922 -1.3357999plot(fit,xvar ="kappa",label =TRUE)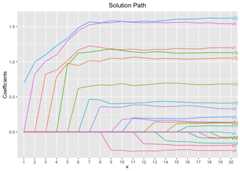

solution path plot for single model fit using L0 penalty for binary data

# Cross-Validation using L1 penaltycv.fit<-cv.glmtlp(bin_data$X, bin_data$y,family ="binomial",penalty ="l1",ncores=2)coef(cv.fit)[abs(coef(cv.fit))>0]#>   intercept          V1          V3          V4          V5          V6#> -0.04597434  0.74281436  0.04345031  0.15993696  0.05100859  0.98672196#>          V8          V9         V10         V13         V15         V19#> -0.04488821 -0.06456282  0.66422939  0.33826482  0.69062166  0.23686317#>         V20#>  1.01116571plot(cv.fit)

cross-validation plot using L1 penalty for binary data

# Single Model Fit using L1 penaltyfit<-glmtlp(bin_data$X, bin_data$y,family ="binomial",penalty ="l1")coef(fit,lambda = cv.fit$lambda.min)#>   intercept          V1          V2          V3          V4          V5#> -0.04597434  0.74281436  0.00000000  0.04345031  0.15993696  0.05100859#>          V6          V7          V8          V9         V10         V11#>  0.98672196  0.00000000 -0.04488821 -0.06456282  0.66422939  0.00000000#>         V12         V13         V14         V15         V16         V17#>  0.00000000  0.33826482  0.00000000  0.69062166  0.00000000  0.00000000#>         V18         V19         V20#>  0.00000000  0.23686317  1.01116571predict(fit,X = bin_data$X[1:5, ],type ="response",lambda = cv.fit$lambda.min)#> [1] 0.35132374 0.90851038 0.03822033 0.93657911 0.03253188plot(fit,xvar ="lambda",label =TRUE)

solution path plot for single model fit using L1 penalty for binary data

Citing information

If you find this project useful, please consider citing

@article{    author = {Chunlin Li, Yu Yang, Chong Wu, Xiaotong Shen, Wei Pan},    title = {{glmtlp: An R package for truncated Lasso penalty}},    year = {2022}}

References

Li, C., Shen, X., & Pan, W. (2021). Inference for a largedirected graphical model with interventions.arXiv preprintarXiv:2110.03805.https://arxiv.org/abs/2110.03805.

Shen, X., Pan, W., & Zhu, Y. (2012). Likelihood-based selectionand sharp parameter estimation.Journal of the American StatisticalAssociation, 107(497), 223-232.https://doi.org/10.1080/01621459.2011.645783.

Shen, X., Pan, W., Zhu, Y., & Zhou, H. (2013). On constrained andregularized high-dimensional regression.Annals of the Institute ofStatistical Mathematics, 65(5), 807-832.https://doi.org/10.1007/s10463-012-0396-3.

Tibshirani, R., Bien, J., Friedman, J., Hastie, T., Simon, N.,Taylor, J., & Tibshirani, R. J. (2012). Strong rules for discardingpredictors in lasso‐type problems.Journal of the Royal StatisticalSociety: Series B (Statistical Methodology), 74(2), 245-266.https://doi.org/10.1111/j.1467-9868.2011.01004.x.

Yang, Y. & Zou, H. A coordinate majorization descent algorithmfor l1 penalized learning.Journal of Statistical Computation andSimulation 84.1 (2014): 84-95.https://doi.org/10.1080/00949655.2012.695374.

Zhu, Y., Shen, X., & Pan, W. (2020). On high-dimensionalconstrained maximum likelihood inference.Journal of the AmericanStatistical Association, 115(529), 217-230.https://doi.org/10.1080/01621459.2018.1540986.

Zhu, Y. (2017). An augmented ADMM algorithm with application to thegeneralized lasso problem.Journal of Computational and GraphicalStatistics, 26(1), 195-204.https://doi.org/10.1080/10618600.2015.1114491.

Part of the code is adapted fromglmnet,ncvreg,andbiglasso.

Warm thanks to the authors of above open-sourcedsoftwares.

[8]ページ先頭
©2009-2025 Movatter.jp