stochvolTMB is a package for fitting stochasticvolatility (SV) models to time series data. It is inspired by thepackagestochvol, butparameter estimates are obtained through optimization and not MCMC,leading to significant speed up. It is built onTemplate Model Builder forfast and efficient estimation. The latent volatility is integrated outof the likelihood using the Laplace approximation and automaticdifferentiation (AD) is used for accurate evaluation of derivatives.
Four distributions for the observational error are implemented:
To install the current stable release from CRAN, use
install.packages("stochvolTMB")To install the current development version, use
# install.packages("remotes")remotes::install_github("JensWahl/stochvolTMB")If you would also like to build and view the vignette locally,use
remotes::install_github("JensWahl/stochvolTMB",dependencies =TRUE,build_vignettes =TRUE)The main function for estimating parameters isestimate_parameters:
library(stochvolTMB,warn.conflicts =FALSE)# load s&p500 data from 2005 to 2018data(spy)# find the best model using AICgaussian<-estimate_parameters(spy$log_return,model ="gaussian",silent =TRUE)t_dist<-estimate_parameters(spy$log_return,model ="t",silent =TRUE)skew_gaussian<-estimate_parameters(spy$log_return,model ="skew_gaussian",silent =TRUE)leverage<-estimate_parameters(spy$log_return,model ="leverage",silent =TRUE)# the leverage model stands out with an AIC far below the other modelsAIC(gaussian, t_dist, skew_gaussian, leverage)#> df AIC#> gaussian 3 -23430.57#> t_dist 4 -23451.69#> skew_gaussian 4 -23440.87#> leverage 4 -23608.85# get parameter estimates with standard errorestimates<-summary(leverage)head(estimates,10)#> parameter estimate std_error z_value p_value type#> 1: sigma_y 0.008338412 0.0004163314 20.0283029 3.121144e-89 transformed#> 2: sigma_h 0.273443559 0.0182641070 14.9716359 1.125191e-50 transformed#> 3: phi 0.967721215 0.0043681868 221.5384240 0.000000e+00 transformed#> 4: rho -0.748695259 0.0322487815 -23.2162340 3.121690e-119 transformed#> 5: log_sigma_y -4.786882463 0.0499293427 -95.8731319 0.000000e+00 fixed#> 6: log_sigma_h -1.296660043 0.0667929683 -19.4131220 5.978190e-84 fixed#> 7: logit_phi 4.110221202 0.1375467861 29.8823500 3.337032e-196 fixed#> 8: logit_rho -1.939958912 0.1467670249 -13.2179481 6.912403e-40 fixed#> 9: h -0.536254072 0.5182192669 -1.0348015 3.007616e-01 random#> 10: h -0.207811236 0.4245258952 -0.4895137 6.244781e-01 random# plot estimated volatility with 95 % confidence intervalplot(leverage,include_ci =TRUE,dates = spy$date)
Given the estimated parameters we can simulate future volatility andlog-returns usingpredict.
set.seed(123)# simulate future prices with or without parameter uncertaintypred=predict(leverage,steps =10)# Calculate the mean, 2.5% and 97.5% quantiles from the simulationspred_summary=summary(pred,quantiles =c(0.025,0.975),predict_mean =TRUE)print(pred_summary)#> $y#> time quantile_0.025 quantile_0.975 mean#> 1: 1 -0.03787452 0.03639606 -2.352005e-04#> 2: 2 -0.03750167 0.03718038 7.938422e-05#> 3: 3 -0.03759011 0.03677040 -6.930858e-05#> 4: 4 -0.03667977 0.03841486 2.810659e-04#> 5: 5 -0.03674431 0.03679402 -1.421016e-04#> 6: 6 -0.03531571 0.03708404 2.750826e-04#> 7: 7 -0.03706161 0.03531337 -9.648350e-05#> 8: 8 -0.03654679 0.03581507 -9.638224e-05#> 9: 9 -0.03558469 0.03600052 -7.431832e-05#> 10: 10 -0.03551163 0.03483791 -3.915279e-04#>#> $h#> time quantile_0.025 quantile_0.975 mean#> 1: 1 0.41447216 2.519873 1.455147#> 2: 2 0.27225022 2.568749 1.408390#> 3: 3 0.10808006 2.612277 1.363972#> 4: 4 0.01248118 2.639010 1.322519#> 5: 5 -0.12153490 2.658716 1.276073#> 6: 6 -0.20817536 2.688433 1.239662#> 7: 7 -0.28558724 2.696168 1.199534#> 8: 8 -0.37711849 2.699062 1.160366#> 9: 9 -0.46776638 2.718274 1.124317#> 10: 10 -0.55249774 2.705546 1.086525#>#> $h_exp#> time quantile_0.025 quantile_0.975 mean#> 1: 1 0.010125271 0.02945742 0.01790539#> 2: 2 0.009421133 0.03039987 0.01765869#> 3: 3 0.008772480 0.03099832 0.01736513#> 4: 4 0.008319762 0.03130376 0.01715038#> 5: 5 0.007848844 0.03163646 0.01677779#> 6: 6 0.007459083 0.03191093 0.01657714#> 7: 7 0.007125009 0.03202311 0.01631264#> 8: 8 0.006833992 0.03228772 0.01612161#> 9: 9 0.006592298 0.03264210 0.01588995#> 10: 10 0.006231481 0.03240400 0.01567428# plot predicted volatility with 0.025 and 0.975 quantilesplot(leverage,include_ci =TRUE,forecast =50,dates = spy$d)+ ggplot2::xlim(c(spy[.N, date]-150, spy[.N, date]+50))#> Warning: Removed 3419 row(s) containing missing values (geom_path).#> Warning: Removed 3419 row(s) containing missing values (geom_path).#> Warning: Removed 3419 row(s) containing missing values (geom_path).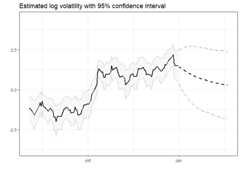
By runningdemo() you start a shiny application whereyou can visually inspect the effect of choosing different models andparameter configurations
demo()