mpoly is a simple collection of tools to help dealwith multivariate polynomialssymbolically and functionally inR. Polynomials are defined with themp() function:
library("mpoly")mp("x + y")# x + ymp("(x + 4 y)^2 (x - .25)")# x^3 - 0.25 x^2 + 8 x^2 y - 2 x y + 16 x y^2 - 4 y^2Termorders are available with the reorder function:
(p<-mp("(x + y)^2 (1 + x)"))# x^3 + x^2 + 2 x^2 y + 2 x y + x y^2 + y^2reorder(p,varorder =c("y","x"),order ="lex")# y^2 x + y^2 + 2 y x^2 + 2 y x + x^3 + x^2reorder(p,varorder =c("x","y"),order ="glex")# x^3 + 2 x^2 y + x y^2 + x^2 + 2 x y + y^2Vectors of polynomials (mpolyList’s) can be specified inthe same way:
mp(c("(x+y)^2","z"))# x^2 + 2 x y + y^2# zYou can extract pieces of polynoimals using the standard[ operator, which works on its terms:
p[1]# x^3p[1:3]# x^3 + x^2 + 2 x^2 yp[-1]# x^2 + 2 x^2 y + 2 x y + x y^2 + y^2There are also many other functions that can be used to piece apartpolynomials, for example the leading term (default lex order):
LT(p)# x^3LC(p)# [1] 1LM(p)# x^3You can also extract information about exponents:
exponents(p)# [[1]]# x y# 3 0## [[2]]# x y# 2 0## [[3]]# x y# 2 1## [[4]]# x y# 1 1## [[5]]# x y# 1 2## [[6]]# x y# 0 2multideg(p)# x y# 3 0totaldeg(p)# [1] 3monomials(p)# x^3# x^2# 2 x^2 y# 2 x y# x y^2# y^2Arithmetic is defined for both polynomials (+,-,* and^)…
p1<-mp("x + y")p2<-mp("x - y")p1+ p2# 2 xp1- p2# 2 yp1* p2# x^2 - y^2p1^2# x^2 + 2 x y + y^2… and vectors of polynomials:
(ps1<-mp(c("x","y")))# x# y(ps2<-mp(c("2 x","y + z")))# 2 x# y + zps1+ ps2# 3 x# 2 y + zps1- ps2# -1 x# -1 zps1* ps2# 2 x^2# y^2 + y zYou can compute derivatives easily:
p<-mp("x + x y + x y^2")deriv(p,"y")# x + 2 x ygradient(p)# y^2 + y + 1# 2 y x + xYou can turn polynomials and vectors of polynomials into functionsyou can evaluate withas.function(). Here’s a basic exampleusing a single multivariate polynomial:
f<-as.function(mp("x + 2 y"))# makes a function with a vector argument# f(.) with . = (x, y)f(c(1,1))# [1] 3f<-as.function(mp("x + 2 y"),vector =FALSE)# makes a function with all arguments# f(x, y)f(1,1)# [1] 3Here’s a basic example with a vector of multivariate polynomials:
(p<-mp(c("x","2 y")))# x# 2 yf<-as.function(p)# f(.) with . = (x, y)f(c(1,1))# [1] 1 2f<-as.function(p,vector =FALSE)# f(x, y)f(1,1)# [1] 1 2Whether you’re working with a single multivariate polynomial or avector of them (mpolyList), if it/they are actuallyunivariate polynomial(s), the resulting function is vectorized. Here’san example with a single univariate polynomial.
f<-as.function(mp("x^2"))# f(.) with . = xf(1:3)# [1] 1 4 9(mat<-matrix(1:4,2))# [,1] [,2]# [1,] 1 3# [2,] 2 4f(mat)# it's vectorized properly over arrays# [,1] [,2]# [1,] 1 9# [2,] 4 16Here’s an example with a vector of univariate polynomials:
(p<-mp(c("t","t^2")))# t# t^2f<-as.function(p)f(1)# [1] 1 1f(1:3)# [,1] [,2]# [1,] 1 1# [2,] 2 4# [3,] 3 9You can use this to visualize a univariate polynomials like this:
library("tidyverse");theme_set(theme_classic())f<-as.function(mp("(x-2) x (x+2)"))# f(.) with . = xx<-seq(-2.5,2.5, .1)qplot(x,f(x),geom ="line")# Warning: `qplot()` was deprecated in ggplot2 3.4.0.# This warning is displayed once every 8 hours.# Call `lifecycle::last_lifecycle_warnings()` to see where this warning was# generated.
For multivariate polynomials, it’s a little more complicated:
f<-as.function(mp("x^2 - y^2"))# f(.) with . = (x, y)s<-seq(-2.5,2.5, .1)df<-expand.grid(x = s,y = s)df$f<-apply(df,1, f)qplot(x, y,data = df,geom ="raster",fill = f)
Usingtidyverse-style coding(install tidyverse packages withinstall.packages("tidyverse")), this looks a bitcleaner:
f<-as.function(mp("x^2 - y^2"),vector =FALSE)# f(x, y)seq(-2.5,2.5, .1)%>%list("x"= .,"y"= .)%>%cross_df()%>%mutate(f =f(x, y))%>%ggplot(aes(x, y,fill = f))+geom_raster()# Warning: `cross_df()` was deprecated in purrr 1.0.0.# ℹ Please use `tidyr::expand_grid()` instead.# ℹ See <https://github.com/tidyverse/purrr/issues/768>.# This warning is displayed once every 8 hours.# Call `lifecycle::last_lifecycle_warnings()` to see where this warning was# generated.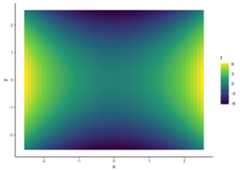
Grobner bases are no longer implemented in mpoly; they’re nowinm2r.
# polys <- mp(c("t^4 - x", "t^3 - y", "t^2 - z"))# grobner(polys)Homogenization and dehomogenization:
(p<-mp("x + 2 x y + y - z^3"))# x + 2 x y + y - z^3(hp<-homogenize(p))# x t^2 + 2 x y t + y t^2 - z^3dehomogenize(hp,"t")# x + 2 x y + y - z^3homogeneous_components(p)# x + y# 2 x y# -1 z^3mpoly can make use of many pieces of thepolynom andorthopolynom packages withas.mpoly() methods. In particular, many special polynomialsare available.
You can constructChebyshevpolynomials as follows:
chebyshev(1)# xchebyshev(2)# -1 + 2 x^2chebyshev(0:5)# 1# x# 2 x^2 - 1# 4 x^3 - 3 x# 8 x^4 - 8 x^2 + 1# 16 x^5 - 20 x^3 + 5 xAnd you can visualize them:
s<-seq(-1,1,length.out =201); N<-5(chebPolys<-chebyshev(0:N))# 1# x# 2 x^2 - 1# 4 x^3 - 3 x# 8 x^4 - 8 x^2 + 1# 16 x^5 - 20 x^3 + 5 xdf<-as.function(chebPolys)(s)%>%cbind(s, .)%>%as.data.frame()names(df)<-c("x",paste0("T_",0:N))mdf<- df%>%gather(degree, value,-x)qplot(x, value,data = mdf,geom ="path",color = degree)
s<-seq(-1,1,length.out =201); N<-5(jacPolys<-jacobi(0:N,2,2))# 1# 5 x# 17.5 x^2 - 2.5# 52.5 x^3 - 17.5 x# 144.375 x^4 - 78.75 x^2 + 4.375# 375.375 x^5 - 288.75 x^3 + 39.375 xdf<-as.function(jacPolys)(s)%>%cbind(s, .)%>% as.data.framenames(df)<-c("x",paste0("P_",0:N))mdf<- df%>%gather(degree, value,-x)qplot(x, value,data = mdf,geom ="path",color = degree)+coord_cartesian(ylim =c(-25,25))
s<-seq(-1,1,length.out =201); N<-5(legPolys<-legendre(0:N))# 1# x# 1.5 x^2 - 0.5# 2.5 x^3 - 1.5 x# 4.375 x^4 - 3.75 x^2 + 0.375# 7.875 x^5 - 8.75 x^3 + 1.875 xdf<-as.function(legPolys)(s)%>%cbind(s, .)%>% as.data.framenames(df)<-c("x",paste0("P_",0:N))mdf<- df%>%gather(degree, value,-x)qplot(x, value,data = mdf,geom ="path",color = degree)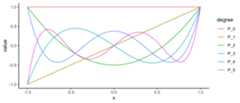
s<-seq(-3,3,length.out =201); N<-5(hermPolys<-hermite(0:N))# 1# x# x^2 - 1# x^3 - 3 x# x^4 - 6 x^2 + 3# x^5 - 10 x^3 + 15 xdf<-as.function(hermPolys)(s)%>%cbind(s, .)%>% as.data.framenames(df)<-c("x",paste0("He_",0:N))mdf<- df%>%gather(degree, value,-x)qplot(x, value,data = mdf,geom ="path",color = degree)
s<-seq(-5,20,length.out =201); N<-5(lagPolys<-laguerre(0:N))# 1# -1 x + 1# 0.5 x^2 - 2 x + 1# -0.1666667 x^3 + 1.5 x^2 - 3 x + 1# 0.04166667 x^4 - 0.6666667 x^3 + 3 x^2 - 4 x + 1# -0.008333333 x^5 + 0.2083333 x^4 - 1.666667 x^3 + 5 x^2 - 5 x + 1df<-as.function(lagPolys)(s)%>%cbind(s, .)%>% as.data.framenames(df)<-c("x",paste0("L_",0:N))mdf<- df%>%gather(degree, value,-x)qplot(x, value,data = mdf,geom ="path",color = degree)+coord_cartesian(ylim =c(-25,25))
Bernsteinpolynomials are not inpolynom ororthopolynom but are available inmpoly withbernstein():
bernstein(0:4,4)# x^4 - 4 x^3 + 6 x^2 - 4 x + 1# -4 x^4 + 12 x^3 - 12 x^2 + 4 x# 6 x^4 - 12 x^3 + 6 x^2# -4 x^4 + 4 x^3# x^4s<-seq(0,1,length.out =101)N<-5# number of bernstein polynomials to plot(bernPolys<-bernstein(0:N, N))# -1 x^5 + 5 x^4 - 10 x^3 + 10 x^2 - 5 x + 1# 5 x^5 - 20 x^4 + 30 x^3 - 20 x^2 + 5 x# -10 x^5 + 30 x^4 - 30 x^3 + 10 x^2# 10 x^5 - 20 x^4 + 10 x^3# -5 x^5 + 5 x^4# x^5df<-as.function(bernPolys)(s)%>%cbind(s, .)%>% as.data.framenames(df)<-c("x",paste0("B_",0:N))mdf<- df%>%gather(degree, value,-x)qplot(x, value,data = mdf,geom ="path",color = degree)
You can use thebernstein_approx() function to computethe Bernstein polynomial approximation to a function. Here’s anapproximation to the standard normal density:
p<-bernstein_approx(dnorm,15,-1.25,1.25)round(p,4)# -0.1624 x^2 + 0.0262 x^4 - 0.002 x^6 + 0.0001 x^8 + 0.3796x<-seq(-3,3,length.out =101)df<-data.frame(x =rep(x,2),y =c(dnorm(x),as.function(p)(x)),which =rep(c("actual","approx"),each =101))# f(.) with . = xqplot(x, y,data = df,geom ="path",color = which)
You can constructBezier polynomialsfor a given collection of points withbezier():
points<-data.frame(x =c(-1,-2,2,1),y =c(0,1,1,0))(bezPolys<-bezier(points))# -10 t^3 + 15 t^2 - 3 t - 1# -3 t^2 + 3 tAnd viewing them is just as easy:
df<-as.function(bezPolys)(s)%>% as.data.frameggplot(aes(x = x,y = y),data = df)+geom_point(data = points,color ="red",size =4)+geom_path(data = points,color ="red",linetype =2)+geom_path(size =2)# Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.# ℹ Please use `linewidth` instead.# This warning is displayed once every 8 hours.# Call `lifecycle::last_lifecycle_warnings()` to see where this warning was# generated.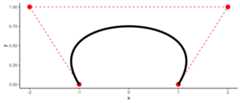
Weighting is available also:
points<-data.frame(x =c(1,-2,2,-1),y =c(0,1,1,0))(bezPolys<-bezier(points))# -14 t^3 + 21 t^2 - 9 t + 1# -3 t^2 + 3 tdf<-as.function(bezPolys,weights =c(1,5,5,1))(s)%>% as.data.frameggplot(aes(x = x,y = y),data = df)+geom_point(data = points,color ="red",size =4)+geom_path(data = points,color ="red",linetype =2)+geom_path(size =2)
To make the evaluation of the Bezier polynomials stable,as.function() has a special method for Bezier polynomialsthat makes use ofdeCasteljau’s algorithm. This allowsbezier() to be usedas a smoother:
s<-seq(0,1,length.out =201)df<-as.function(bezier(cars))(s)%>% as.data.frameqplot(speed, dist,data = cars)+geom_path(data = df,color ="red")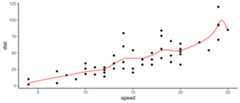
I’m starting to put in methods for some other R functions:
set.seed(1)n<-101df<-data.frame(x =seq(-5,5,length.out = n))df$y<-with(df,-x^2+2*x-3+rnorm(n,0,2))mod<-lm(y~ x+I(x^2),data = df)(p<- mod%>% as.mpoly%>% round)# 1.983 x - 1.01 x^2 - 2.709qplot(x, y,data = df)+stat_function(fun =as.function(p),colour ='red')# f(.) with . = x
s<-seq(-5,5,length.out = n)df<-expand.grid(x = s,y = s)%>%mutate(z = x^2- y^2+3*x*y+rnorm(n^2,0,3))(mod<-lm(z~poly(x, y,degree =2,raw =TRUE),data = df))## Call:# lm(formula = z ~ poly(x, y, degree = 2, raw = TRUE), data = df)## Coefficients:# (Intercept) poly(x, y, degree = 2, raw = TRUE)1.0# -0.070512 -0.004841# poly(x, y, degree = 2, raw = TRUE)2.0 poly(x, y, degree = 2, raw = TRUE)0.1# 1.005307 0.001334# poly(x, y, degree = 2, raw = TRUE)1.1 poly(x, y, degree = 2, raw = TRUE)0.2# 3.003755 -0.999536as.mpoly(mod)# -0.004840798 x + 1.005307 x^2 + 0.001334122 y + 3.003755 x y - 0.9995356 y^2 - 0.07051218From CRAN:install.packages("mpoly")
From Github (dev version):
# install.packages("devtools")devtools::install_github("dkahle/mpoly")This material is based upon work partially supported by the NationalScience Foundation under Grant No. 1622449.