サクサク読めて、
アプリ限定の機能も多数!

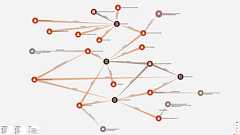
世界中で話題になっているパナマ文書。各国で政権を揺るがすような事態にもなっていますが、純粋にデータとしてみた場合、これは計算機やデータ解析に関わる人々にも面白いものだと思います。データの中身や背景などについてはさんざん報道されていますのでここでは触れません。一方、現場でどのような作業が行われているのかはあまり報道されていません。現実的な問題として、人力ではどうしようもない量のリークデータを手に入れた場合、調査報道機関はどんなことを行っているのでしょうか?私も以前から疑問に思っていたのですが、先日あるデータベース企業と、データ分析アプリケーションを作成する会社のブログにて、その実際の一端を窺うことができる投稿がありました: Panama Papers: How Linkurious enables ICIJ to investigate the massive Mossack Fonseca
The document discusses algorithms for finding minimum spanning trees in graphs.It describes Prim's and Kruskal's algorithms, which both run in O(ElogV) time where E is the number of edges and V is the number of vertices.It also mentions that Fibonacci heaps can be used to implement Prim's algorithm in O(E+VlogV) time.

For thenetwork protocol, see Spanning Tree Protocol. For other uses, see Spanning tree (disambiguation). A spanning tree (blue heavy edges) of a grid graph In the mathematical field of graph theory, a spanning tree T of an undirected graph G is a subgraph that is a tree which includes all of the vertices of G.[1] In general, a graph may have several spanning trees, but a graph that is not connect

最小全域木問題を解くためのアルゴリズム「クラスカル法」と「プリム法」を使ってみた. 最小全域木について クラスカル法 プリム法 PKUの問題 クラスカル法による解答 プリム法による解答 メモリ使用量と実行時間の比較 最小全域木について まず,全域木(Spanning tree)とは連結グラフの全ての頂点とそのグラフを構成する辺の一部分のみで構成される木のこと.つまり,連結グラフから適当な辺を取り除いていき,閉路をもたない木の形にしたものが全域木となる.ここで,グラフの各辺に重みがある場合,重みの総和が最小になるように辺を選んで作った全域木のことを最小全域木(Minimum spanning tree)という. 最小全域木を求めるアルゴリズムとしては以下の二つが有名である. クラスカル法 (Kruskal's algorithm) プリム法 (Prim's algorithm) いずれも貪欲
このブログにはGvizに関する大量の記述があるのだけれどもまともにタグ付けされてないサイト検索もできないと非常にアクセスビリティの悪い有り様でまあ本来なら気合を入れてひとつその全体解説たる記事を書き下ろしてここに公開!と宣言してついでにEPUBにまとめて一攫千金と相成りたいところ如何せん筆がぁ筆がぁっつって一向に気持ちがそちら方面に向かわずにおるわけで。 そこで代わりといってはなんですが「Gvizの目次 -Rubyの世界からGraphvizの世界にこんにちは!」と題して過去の記事をここにまとめて一覧できるように致しましたのでGvizをご利用頂いていていままで右往左往させられていた方あるいは使い方がわからん何が描けるのかわからん全く意味がわからんという方あるいは将来においてGvizに興味を持たれる可能性のある方居られましたら是非ともこのページを基点として各ページに飛んで頂きたくお願い申し上

アリーナの現バージョンは, 前バージョンとくらべ, 以下の点が変更されています。 1.アリーナは C# 言語,Java 言語にくわえ,JavaScript 言語でも利用できるようになりました。 2.グラフデータのファイルコードを, シフト JIS コードからUTF-8 コードに変更しました。 3.G.EachVertex など Each が接頭語になっているメソッドをなくしました。 4.データメンバのアクセス法を, プロパティによる方法からメソッドによる方法に変更しました。 例:v.X を v.GetX(),v.SetX(x) に。 G.Vertices を G.Vertices() に。 5.メソッドの命名規則を変更しました。 例:G.Remove(v),G.Remove(e) を G.RemoveVertex(v),G.RemoveEdge(e) に。
The source for financial, economic, and alternative datasets, serving investment professionals.

はじめにGoogle Summer of Code 2014にSciRubyの学生として参加していました。 3か月の期間が無事終了し、ちゃんとした成果物ができたので記事にします。 Nyaplotについて、コードや詳しい使い方はこちらをご覧ください: domitry/nyaplot ·GitHub domitry/Nyaplotjs ·GitHub あーなんか余裕なかったなあとかGSoCの感想みたいなのはまた落ち着いてから書こうかと思います。 概要 IRubynotebook上で動作する、plotのためのgem。 すごいところ インタラクティブな/インタラクティブにplotができる。 IRubynotebook上で対話的にプロットを作ることができます。また標準で用意される様々なモジュールがユーザーの対話的な操作を支援します。 作ったプロットはSVGやWebGLを使いブラウザ上に表示
私たちは、さまざまな革新的製品と有用な技術を用いて化学合成ワークフローにあらゆるソリューションを提供します。創薬スクリーニングやメディシナルケミストリーへの応用から、さまざまな合成手法、バイオコンジュゲーション、標的タンパク質分解まで、お客様の有機化学、有機金属化学およびケミカルバイオロジーのあらゆる用途や手法をサポートします。
Velvet や ABySS などの代表的な de novo アセンブリツールでは、アルゴリズムに de Bruijn Graph というのを使っているそうです。どうやってアセンブルしているんだろう?と興味を持っていたので、元ネタの An Eulerian path approach to DNA fragment assembly を読んでみたんですが、その発想のすごさに度肝を抜かれました。せっかくなので、ここで簡単に説明してみたいと思います。 ケーニヒスベルクの橋 まずはグラフ理論の説明から。グラフ理論は、18世紀にオイラーという数学者が「ケーニヒスベルクの橋」という問題を解くために考え出したといわれています。 「ケーニヒスベルクの橋」は、次のような問題です。 18世紀の初めごろにプロイセン王国の首都であるケーニヒスベルクという大きな町があった。この町の中央には、プレーゲル川という大き


Deleted articles cannot be recovered. Draft of this article would be also deleted. Are you sure you want to delete this article? このシリーズは、Cytoscapeを使ってやIPythonNotebook、Pandasなどのオープンソースツールを利用し、公開データを元に実際のグラフ可視化を行う過程を紹介する、可視化の実践者向けの記事です。 第一回 第二回 第三回 第四回 Cytoscapeを使った実際の可視化作業の流れ はじめに 誰にでも馴染みのある公開データを使って単純な例を作ろうと思い始めた今回の作業ですが、思いのほかデータ加工が面倒で、実際の可視化作業の解説まで時間がかかってしまいました。今回はいよいよPythonスクリプトから出力されたデータを使い、ファ

 1
1リリース、障害情報などのサービスのお知らせ
最新の人気エントリーの配信
処理を実行中です
j次のブックマーク
k前のブックマーク
lあとで読む
eコメント一覧を開く
oページを開く